All posts by Andy Wheeler

Labeling tricks in SPSS plots

The other day I noticed when making the labels for treemaps that when using a polygon element in inline GPL SPSS places the label directly on the centroid. This is opposed to offsetting the label when using a point element. We can use this to our advantage to force labels in plots to be exactly where we want them. (Syntax to replicate all of this here.)

One popular example I have seen is in state level data to use the state abbreviation in a scatterplot instead of a point. Here is an example using the college degree and obesity example originally via Albert Cairo.

FILE HANDLE save /NAME = "!!!!Your Handle Here!!!".
*Data obtained from http://vizwiz.blogspot.com/2013/01/alberto-cairo-three-steps-to-become.html
*Data was originally from VizWiz blog https://dl.dropbox.com/u/14050515/VizWiz/obesity_education.xls.
*That link does not work anymore though, see https://www.dropbox.com/s/lfwx7agkraci21y/obesity_education.xls?dl=0.
*For my own dropbox link to the data.
GET DATA /TYPE=XLS
   /FILE='save\obesity_education.xls'
   /SHEET=name 'Sheet1'
   /CELLRANGE=full
   /READNAMES=on
   /ASSUMEDSTRWIDTH=32767.
DATASET NAME Obs.
MATCH FILES FILE = *
/DROP V5.
FORMATS BAORHIGHER OBESITY (F2.0).

*Scatterplot with States and labels.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BAORHIGHER OBESITY StateAbbr
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BAORHIGHER=col(source(s), name("BAORHIGHER"))
  DATA: OBESITY=col(source(s), name("OBESITY"))
  DATA: StateAbbr=col(source(s), name("StateAbbr"), unit.category())
  GUIDE: axis(dim(1), label("% BA or Higher"))
  GUIDE: axis(dim(2), label("% Obese"))
  ELEMENT: point(position(BAORHIGHER*OBESITY), label(StateAbbr))
END GPL.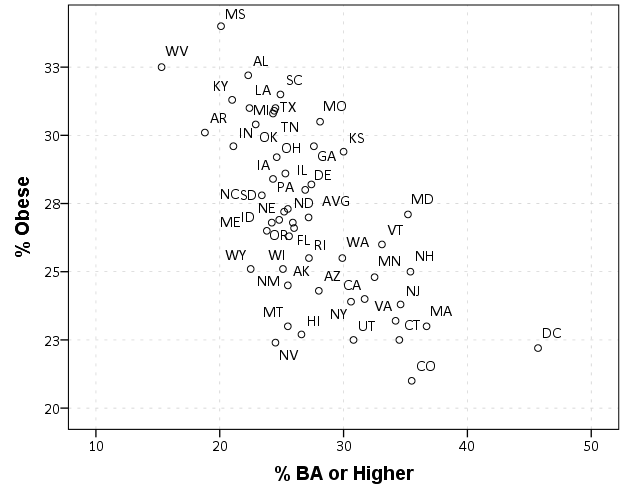

Here you can see the state abbreviations are off-set from the points. A trick to just plot the labels, but not the points, is to draw the points fully transparent. See the transparency.exterior(transparency."1") in the ELEMENT statement.

 GGRAPH
   /GRAPHDATASET NAME="graphdataset" VARIABLES=BAORHIGHER OBESITY StateAbbr
   /GRAPHSPEC SOURCE=INLINE.
 BEGIN GPL
   SOURCE: s=userSource(id("graphdataset"))
   DATA: BAORHIGHER=col(source(s), name("BAORHIGHER"))
   DATA: OBESITY=col(source(s), name("OBESITY"))
   DATA: StateAbbr=col(source(s), name("StateAbbr"), unit.category())
   GUIDE: axis(dim(1), label("% BA or Higher"))
   GUIDE: axis(dim(2), label("% Obese"))
   ELEMENT: point(position(BAORHIGHER*OBESITY), label(StateAbbr), 
            transparency.exterior(transparency."1"))
 END GPL.

But, this does not draw the label exactly at the data observation. You can post-hoc edit the chart to specify that the label is drawn at the middle of the point element, but another option directly in code is to specify the element as a polygon instead of a point. By default this is basically equivalent to using a point element, since we do not pass the function an actual polygon using the link.??? functions.

GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BAORHIGHER OBESITY StateAbbr
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BAORHIGHER=col(source(s), name("BAORHIGHER"))
  DATA: OBESITY=col(source(s), name("OBESITY"))
  DATA: StateAbbr=col(source(s), name("StateAbbr"), unit.category())
  GUIDE: axis(dim(1), label("% BA or Higher"))
  GUIDE: axis(dim(2), label("% Obese"))
  ELEMENT: polygon(position(BAORHIGHER*OBESITY), label(StateAbbr), transparency.exterior(transparency."1"))
END GPL.

To show that this now places the labels directly on the data values, here I superimposed the data points as red dots over the labels.

GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BAORHIGHER OBESITY StateAbbr
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BAORHIGHER=col(source(s), name("BAORHIGHER"))
  DATA: OBESITY=col(source(s), name("OBESITY"))
  DATA: StateAbbr=col(source(s), name("StateAbbr"), unit.category())
  GUIDE: axis(dim(1), label("% BA or Higher"))
  GUIDE: axis(dim(2), label("% Obese"))
  ELEMENT: polygon(position(BAORHIGHER*OBESITY), label(StateAbbr), transparency.exterior(transparency."1"))
  ELEMENT: point(position(BAORHIGHER*OBESITY), color.interior(color.red))
END GPL.

Note to get the labels like this my chart template specifies the style of data labels as:

 <!-- Custom data labels for points -->
 <setGenericAttributes elementName="labeling" parentName="point" count="0" styleName="textFrameStyle" color="transparent" color2="transparent"/>

The first style tag specifies the font, and the second specifies the background color and outline (my default was originally a white background with a black outline). The option styleOnly="true" makes it so the labels are not always generated in the chart. Another side-effect of using a polygon element I should note is that SPSS draws all of the labels. When labelling point elements SPSS does intelligent labelling, and does not label all of the points if many overlap (and tries to place the labels at non-overlapping locations). It is great for typical scatterplots, but here I do not want that behavior.

Other examples I think this would be useful are for simple dot plots in which the categories have meaningful labels. Here is an example using a legend, and one has to learn the legend to understand the graph. I like making the points semi-transparent, so when they overlap you can still see the different points (see here for an example with data that actually overlap).

Such a simple graph though we can plot the category labels directly.

The direct labelling will not work out so well if if many of the points overlap, but jittering or dodging can be used then as well. (You will have to jitter or dodge the data yourself if using a polygon element in inline GPL. If you want to use a point element again you can post hoc edit the chart so that the labels are at the middle of the point.)

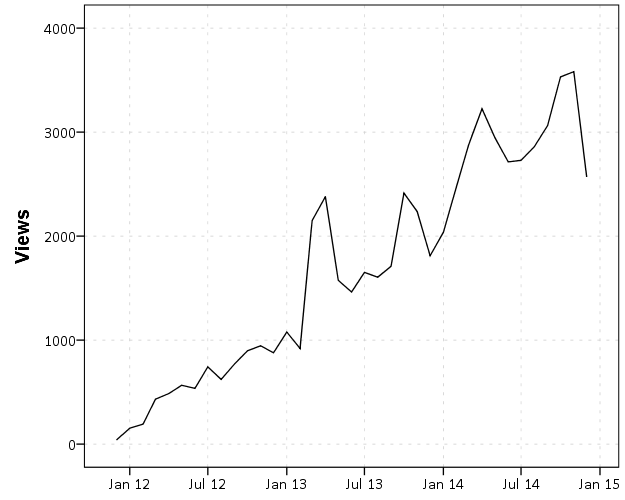
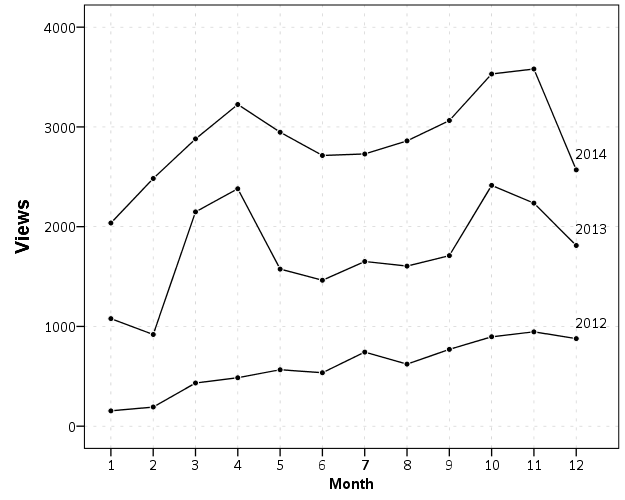
Another example is that I like to place labels in line graphs at the end of the line. Here I show an example of doing that by making a separate label for only the final value of the time series, offsetting to the right slightly, and then placing the invisible polygon element in the chart.

SET SEED 10.
INPUT PROGRAM.
LOOP #M = 1 TO 5.
  LOOP T = 1 TO 10.
    COMPUTE ID = #M.
    COMPUTE Y = RV.NORMAL(#M*5,1).
    END CASE.
  END LOOP.
END LOOP.
END FILE.
END INPUT PROGRAM.
DATASET NAME TimeSeries.
FORMATS T ID Y (F3.0).
ALTER TYPE ID (A1).

STRING Lab (A1).
IF T = 10 Lab = ID.
EXECUTE.

*Labelled at end of line.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=T Y ID Lab MISSING=VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: T=col(source(s), name("T"))
  DATA: Y=col(source(s), name("Y"))
  DATA: ID=col(source(s), name("ID"), unit.category())
  DATA: Lab=col(source(s), name("Lab"), unit.category())
  TRANS: P=eval(T + 0.2)
  GUIDE: axis(dim(1), label("T"))
  GUIDE: axis(dim(2), label("Y"))
  SCALE: linear(dim(1), min(1), max(10.2))
  ELEMENT: line(position(T*Y), split(ID))
  ELEMENT: polygon(position(P*Y), label(Lab), transparency.exterior(transparency."1"))
END GPL.

This works the same for point elements too, but this forces the label to be drawn and they are drawn at the exact location. See the second image in my peremptory challenge post for example behavior when labelling with the point element.

You can also use this to make random annotations in the graph. Code omitted here (it is available in the syntax at the beginning), but here is an example:

If you want you can then style this label separately when post-hoc editing the chart. Here is a silly example. (The workaround to use annotations like this suggests a change to the grammar to allow GUIDES to have a special type specifically for just a label where you supply the x and y position.)

This direct labelling just blurs the lines between tables and graphs some more, what Tukey calls semi-graphic. I recently came across the portmanteau, grables (graphs and tables) to describe such labelling in graphs as well.

 

3 Comments
by Andy Wheeler on January 14, 2015  •  Permalink
Posted in Data Visualization, SPSS
Tagged , ,

Posted by Andy Wheeler on January 14, 2015

https://andrewpwheeler.com/2015/01/14/labeling-tricks-in-spss-plots/

Translating between the dispersion term in a negative binomial regression and random variables in SPSS

NOTE!! – when I initially posted this I was incorrect, I thought SPSS listed the dispersion term in the form of Var(x) = mean + mean*dispersion. But I was wrong, and it is Var(x) = 1 + mean*dispersion (the same as Stata’s, what Cameron and Trivedi call the NB2 model, as cited in the Long and Freese Stata book for categorical variables.) The simulation in the original post worked out because my example I used the mean as 1, here I update it to have a mean of 2 to show the calculations are correct. (Also note that this parametrization is equivalent to Var(x) = mean*(1 + mean*dispersion), see Stata’s help for nbreg.)

When estimating a negative binomial regression equation in SPSS, it returns the dispersion parameter in the form of:

Var(x) = 1 + mean*dispersion

When generating random variables from the negative binomial distribution, SPSS does not take the parameters like this, but the more usual N trials with P successes. Stealing a bit from the R documentation for dnbinom, I was able to translate between the two with just a tedious set of algebra. So with our original distribution being:

Mean = mu
Variance = 1 + mu*a

R has an alternative representation closer to SPSS’s based on:

Mean = mu
Variance = mu + mu^2/x

Some tedious algebra will reveal that in this notation x = mu^2/(1 - mu + a*mu) (note to future self, using Solve in Wolfram Alpha could have saved some time, paper and ink). Also, R’s help for dbinom states that in the original N and P notation that p = x/(x + mu). So here with mu and a (again a is the dispersion term as reported by GENLIN in SPSS) we can solve for p.

x = mu^2/(1 - mu + a*mu)
p = x/(x + mu)

And since p is solved, R lists the mean of the distribution in the N and P notation as:

n*(1-p)/p = mu

So with p solved we can figure out N as equal to:

mu*p/(1-p) = n

So to reiterate, if you have a mean of 2 and dispersion parameter of 4, the resultant N and P notation would be:

mu = 2
a = 4
x = mu^2/(1 - mu + a*mu) = 2^2/(1 - 2 + 4*2) = 4/7
p = x/(x + mu) = (4/7)/(4/7 + 2) = 2/9
n = mu*p/(1-p) = 2*(2/9)/(7/9) = 4/7

Here we can see that in the N and P notation the similar negative binomial model results in a fractional number of successes, which might be a surprising result for some that it is even a possibility. (There is likely an easier way to do this translation, but forgive me I am not a mathematician!)

Now we would be finished, but unfortunately SPSS’s negative binomial random functions only take integer values and do not take values of N less than 1 (R’s dnbinom does). So we have to do another translation of the N and P notation to the gamma distribution to be able to draw random numbers in SPSS. Another representation of the negative binomial model is a mixture of Poisson distributions, with the distribution of the mixtures being from a gamma distribution. Wikipedia lists a translation from the N and P notation to a gamma with shape = N and scale = P/(1-P).

So I wrapped these computations up in an SPSS macros that takes the mean and the dispersion parameter, calculates N and P under the hood, and then draws a random variable from the associated negative binomial distribution.

DEFINE !NegBinRV (mu = !TOKENS(1)
       /disp = !TOKENS(1) 
       /out = !TOKENS(1) )
COMPUTE #x = !mu**2/(1 - !mu + !disp*!mu).
COMPUTE #p = #x / (#x + !mu).
COMPUTE #n = !mu*#p/(1 - #p).
COMPUTE #G = RV.GAMMA(#n,#p/(1 - #p)).
COMPUTE !Out = RV.POISSON(#G).
FORMATS !Out (F5.0).
!ENDDEFINE.

I am not sure if it is possible to use this gamma representation and native SPSS functions to calculate the corresponding CDF and PDF of the negative binomial distribution. But we can use R to do that. Here is an example of keeping the mean at 1 and varying the dispersion parameter between 0 and 5.

BEGIN PROGRAM R.
library(ggplot2)
x <- expand.grid(0:10,1:5)
names(x) <- c("Int","Disp")
mu <- 1
x$PDF <- mapply(dnbinom, x=x$Int, size=mu^2/(1 - mu + x$Disp*mu), mu=mu)
#add in poisson 
t <- data.frame(cbind(0:10,rep(0,11),dpois(0:10,lambda=1)))
names(t) <- c("Int","Disp","PDF")
x <- rbind(t,x)
p <- ggplot(data = x, aes(x = Int, y = PDF, group = as.factor(Disp))) + geom_line()
p
#for the CDF
x$CDF <- ave(x$PDF, x$Disp, FUN = cumsum) 
END PROGRAM.

Here you can see how the larger dispersion term can easily approximate the zero inflation typical in criminal justice data (see an applied example from my work). R will not take a dispersion parameter of zero in this notation (as the size would be divided by zero and not defined), so I just tacked on the Poisson distribution with a mean of zero.

Here is an example of generating random data from a negative binomial distribution with a mean of 2 and a dispersion parameter of 4. I then grab the PDF from R, and superimpose them both on a chart in SPSS (or perhaps I should call it a PMF, since it only has support on integer values). You can see the simulation with 10,000 observations is a near perfect fit (so a good sign I did not make any mistakes!)

*Simulation In SPSS.
INPUT PROGRAM.
LOOP Id = 1 TO 10000.
END CASE.
END LOOP.
END FILE.
END INPUT PROGRAM.
DATASET NAME RandNB.

!NegBinRV mu = 2 disp = 4 out = NB.

*Making seperate R dataset of PDF.
BEGIN PROGRAM R.
mu <- 2
disp <- 4
x <- 0:11
pdf <- dnbinom(x=x,size=mu^2/(1 - mu + disp*mu),mu=mu)
#add in larger than 10
pdf[max(x)+1] <- 1 - sum(pdf[-(max(x)+1)])
MyDf <- data.frame(cbind(x,pdf))
END PROGRAM.
EXECUTE.
STATS GET R FILE=* /GET DATAFRAME=MyDf DATASET=PDF_NB.
DATASET ACTIVATE PDF_NB.
FORMATS x (F2.0).
VALUE LABELS x 11 '11 or More'.

*Now superimposing bar plot and PDF from separate datasets.
DATASET ACTIVATE RandNB.
RECODE NB (11 THRU HIGHEST = 11)(ELSE = COPY) INTO NB_Cat.
FORMATS NB_Cat (F2.0).
VALUE LABELS NB_Cat 11 '11 or More'.

GGRAPH
  /GRAPHDATASET NAME="Data" DATASET='RandNB' VARIABLES=NB_Cat[LEVEL=ORDINAL] COUNT()[name="COUNT"] 
  /GRAPHDATASET NAME="PDF" DATASET='PDF_NB' VARIABLES=x pdf
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: Data=userSource(id("Data"))
  DATA: NB_Cat=col(source(Data), name("NB_Cat"), unit.category())
  DATA: COUNT=col(source(Data), name("COUNT"))
  SOURCE: PDF=userSource(id("PDF"))
  DATA: x=col(source(PDF), name("x"), unit.category())
  DATA: den=col(source(PDF), name("pdf"))
  TRANS: den_per = eval(den*100)
  GUIDE: axis(dim(1))
  GUIDE: axis(dim(2))
  SCALE: linear(dim(2), include(0))
  ELEMENT: interval(position(summary.percent(NB_Cat*COUNT)), shape.interior(shape.square))
  ELEMENT: point(position(x*den_per), color.interior(color.black), size(size."8"))
END GPL.
2 Comments
by Andy Wheeler on January 3, 2015  •  Permalink
Posted in Macro, Regression, SPSS
Tagged , ,

Posted by Andy Wheeler on January 3, 2015

https://andrewpwheeler.com/2015/01/03/translating-between-the-dispersion-term-in-a-negative-binomial-regression-and-random-variables-in-spss/

2014 Blog stats, and why Blogging >> Articles

The readership of the blog has continued to grow. Here are the total site views per month since the beginning in December 2011.

At this point we can start to see some seasonal patterns. I take a big hit in December and January, and increases when school is in session. I get quite a bit of my traffic from SPSS searches, so I presume much of the traffic are students using SPSS.

I do not worry too much about posting regularly, but I like to take some time if I have not published anything in around 2 weeks. I just enjoy taking a break from a specific work projects, and often I blog about something I have dealt with multiple times (or answered peoples questions multiple times) so I like making a blog post for my own and others reference.

Now, one of the more popular posts I have written is Odds Ratios NEED To Be Graphed On Log Scales. This I published in October 2013, recieved around 100 referrals from twitter the day I published it, and since has averaged about 5-10 views per day (it has accumulated a total of near 3,000 total). It is one of the first sites returned for odds ratio graph from a google search.

Certainly not a number of views to write home to my mother about, but I believe it is better outreach of my opinion than a journal article (not that I would be able to publish such a limited point in a journal article anyway). Take for instance Rothman et al.’s 2011 article, Should Graphs of Risk or Rate Ratios be Plotted on a Log Scale? in the American Journal of Epidemiology that has a differing opinion of mine. I can not find any readership stats for AJE, but I highly doubt that article has been viewed by 3,000 people, and according to google scholar it only has 2 citations currently. One is the response by the editor to the article, and the other is likely in error as it was published before the Rothman article. Site views are superficial as well, but I would place a wager my blog post has reached more readers than the Rothman article. 3,000 is way higher than views or downloads for my papers on SSRN, and even the most viewed articles since 2011 on the Cartography and GIS website have not accumulated 3,000 downloads at this point. (My Viz JTC paper has just over 100 downloads so far after being up for close to a year at this point.) AJE articles very likely have a larger readership than CaGIS – but I have no idea how much larger. I would guess the American Statistician has a more comparable (likely larger?) membership via the ASA, and articles from the first issue of 2014 have accumulated mostly between 200 and 1500 downloads currently (the last issue of 2013 is quite a bit lower). I suspect a download is a bit more of an investment than a page view of my blog (so both are over-estimates of those actually reading the article, but page views are likely a larger over-estimate). But in most cases I get so many more views on the blog compared to that I would an article outreach on the blog is clearly the winner. The audience is different as well, not necessarily better or worse, just different.

I don’t take my work as venerable as Ken Rothman’s (obviously he is a well respected and influential epidemiologist or methodologist more generally for his books), but I disagree with his reasoning for using linear scales in some circumstances in the referenced article. My general response to the Rothman example is that if you want to show absolute risk differences then show them. Plotting the ratios on an arithmentic scale is misleading, and while close for his example is still not as accurate as just plotting the risk differences. In Rothman et al.’s example plotting the odds ratios would result in an overestimate of the absolute risk differences by over 10%! (The absolute risk difference is 90 - 1 = 89, whereas the linear difference between the odds is 10 - .01 = 9.99. The former mapped onto a scale from 0 to 10 would result in a length of 8.9, so an over estimate of (9.99 - 8.9)/8.9 ~ 12%.)

I don’t take blogging as a replacement for academic work, more like an open nerd journal. I’m pretty sure this venue has quite a bit more readership than my journal articles ever will though.

 

1 Comment
by Andy Wheeler on January 2, 2015  •  Permalink
Posted in Meta, scholarly
Tagged ,

Posted by Andy Wheeler on January 2, 2015

https://andrewpwheeler.com/2015/01/02/2014-blog-stats-and-why-blogging-articles/

Treemaps in SPSS

Instead of an Xmas tree this year I will discuss a bit about treemaps. Treemaps are a visualization developed by Ben Shneiderman to identify how the current space on ones hard drive is being partitioned. Now they are a popular tool to visualize any hierarchical data that have quantitative size data associated with it. Some of my favorites are from Catherine Mulbrandon of the Visualizing Economics blog. Here is one visualizing the job market sector:

There are quite a few problems with visualizing treemaps, mainly that evaluating areas are a much more difficult task than evaluating the position along an aligned axis. I find some of them visually appealing though, and well suited for their original goal: identifying large categories in unordered hierarchical data with very many categories. So I took some time to write up code to make them in SPSS. The layout algorithm I use (I believe) is the slice and dice, which does not look nice if there are many small categories, but basically a nice workaround is to create different levels in the hierarchy. (This took me about 4+ hours to do, and at this point I would just use a Python or R library to make them if I wanted a different layout algorithm.)

So here is the macro in an sps file (plus the other files used in this post), and it takes as parameters:

  • Data: the name of the original dataset
  • Val (optional): If your categorical data have a numeric variable indicating the size of the category. If not, it simply counts up the number of times a category is in the data file.
  • Vars: the categorical variables that define the treemap. (This should work with as many categories as you want, tested currently with up to 4.)

So lets make some fake data, load in the macro, and then see what it spits out.

FILE HANDLE data /NAME = "C:\Users\andrew.wheeler\Dropbox\Documents\BLOG\TreeMaps_SPSS".
INSERT FILE = "data\TreeMap_MACRO.sps".
*Making some random data.
SET SEED 10.
INPUT PROGRAM.
LOOP #i = 1 TO 1000.
  COMPUTE Cat1 = RV.UNIFORM(0,1).
  COMPUTE Cat2 = RV.UNIFORM(0,1).
  END CASE.
END LOOP.
END FILE.
END INPUT PROGRAM.
DATASET NAME Tree.
NUMERIC C1 C2.
DO REPEAT Prop1 = 0.6 0.9 0.97 1
         /Prop2 = 0.4 0.7 0.9 1
         /i = 1 TO 4.
  IF (MISSING(C1) AND Cat1 <= Prop1) C1 = i.
  IF (MISSING(C2) AND Cat2 <= Prop2) C2 = i.
END REPEAT.
COMPUTE C3 = RV.BERNOULLI(0.8).
MATCH FILES FILE = * /DROP Cat1 Cat2.
FORMATS C1 C2 C3 (F1.0).
EXECUTE.
*Making the rectangles.
!TreeMap Data = Tree Vars = C1 C2 C3.

You have returned a second dataset named Tree_C3 that contains the corners of the boxes for each level of the hierarchy in a set of variables BL_x, BL_y, TR_x, TR_y (meant to be bottom left x, top right y etc.) Using the link.hull parameter for a polygon element in inline GPL (as I showed for spineplots) we can now create the boxes.

*Now plotting the rectangles.
MATCH FILES FILE = * 
  /FIRST = Flag
  /BY C1 C2.
DO IF Flag = 0.
  DO REPEAT x = BL_x2 BL_y2 TR_x2 TR_y2.
    COMPUTE x = $SYSMIS.
  END REPEAT.
END IF.
*Prevents repeated drawing of the same polygon at a higher level.
EXECUTE.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BL_x3 BL_y3 TR_x3 TR_y3 BL_x2 BL_y2 TR_x2 TR_y2 C1 C2 C3 
                MISSING=VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE TEMPLATE = "data\Labels_Poly.sgt".
BEGIN GPL
  PAGE: begin(scale(800px,600px))
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BL_x3=col(source(s), name("BL_x3"))
  DATA: BL_y3=col(source(s), name("BL_y3"))
  DATA: TR_x3=col(source(s), name("TR_x3"))
  DATA: TR_y3=col(source(s), name("TR_y3"))
  DATA: BL_x2=col(source(s), name("BL_x2"))
  DATA: BL_y2=col(source(s), name("BL_y2"))
  DATA: TR_x2=col(source(s), name("TR_x2"))
  DATA: TR_y2=col(source(s), name("TR_y2"))
  DATA: C1=col(source(s), name("C1"), unit.category())
  DATA: C2=col(source(s), name("C2"), unit.category())
  DATA: C3=col(source(s), name("C3"), unit.category())
  TRANS: casenum = index()
  SCALE: cat(aesthetic(aesthetic.texture.pattern), map(("0",texture.pattern.mesh),("1",texture.pattern.solid)))
  GUIDE: legend(aesthetic(aesthetic.color.interior), label("Cat 1"))
  GUIDE: legend(aesthetic(aesthetic.texture.pattern), label("Cat 3"))
  GUIDE: axis(dim(1), null())
  GUIDE: axis(dim(2), null())
  ELEMENT: polygon(position(link.hull((BL_x3 + TR_x3)*(BL_y3 + TR_y3))), split(C2), color.interior(C1),
           texture.pattern(C3))
  ELEMENT: polygon(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))), transparency.exterior(transparency."1"),
           transparency.interior(transparency."1"), label(C2), split(casenum))
  ELEMENT: edge(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))), size(size."3"), split(casenum))
  PAGE: end()
END GPL.

So here is a quick rundown of the complicated GPL code. Here I mapped colors to the first C1 category, and then made C3 a different texture pattern. To get all of the squares to draw I use the split modifier on the C2 category, which has no direct aesthetics mapped, and then placed the C2 label in the center. I made the labels white with an additional chart template to my default, and made the outline for the C2 bars more distinct by plotting them on top as an edge element and making them thicker. If I wanted to publish this, I would probably just export the vector chart and add in the labels in nice spots (SPSS I don’t believe you can style the labels separately, maybe you can with some chart template magic that I am unaware of). So here if I could in SPSS I would make the labels for category 1 in the top left of its respective color, but that is not possible.

If we change the categories to not be so uneven, you can see how my slice-and-dice layout algorithm is not so nice. Here it is with the proportions being about equal for all categories.

Fortunately most categorical data are not like this, and have uneven distributions (also with even data and more hierarchies it tends to look nicer). For an actual example, I grabbed the NIBRS 2012 incident data from ICPSR, which is incident level crime reports from participating police jurisdictions over the country (NIBRS stands for National Incident Based Reporting System). It is pretty big, over 5 million records, and with the over 350 variables the fixed text file is over 6 gigabytes, but the compressed zsav format is only slightly larger than the original gzipped file from ICPSR, (0.35 gigabytes vs 0.29 gigabytes in the fixed width ascii gzipped). So here I grab the NIBRS data I prepared, and create the hierarchy as follows:

  • Level 1: I aggregate the UCR crimes into Part 1 Violent, Part 1 Non-Violent, and Other
  • Level 2: Individual UCR categories
  • Level 3: Location Type broken down into outdoor, indoor, home, and other/missing

And here is the code and the plot:

*Now NIBRS data.
DATASET CLOSE ALL.
GET FILE = "data\NIBRS_2012.zsav".
DATASET NAME NIBRS_2012.

RECODE V20061 (91 THRU 132 = 1)(200 THRU 240 = 2)(ELSE = 3) INTO UCR_Cat.
VALUE LABELS UCR_Cat 1 'Violent' 2 'Property' 3 'Other'.
RECODE V20111 (10,13,16,18,50,51 = 1)(20 = 3)(25, LO THRU 0 = 4)(ELSE = 2) INTO Loc_Cat.
VALUE LABELS Loc_Cat 1 'Outdoor' 2 'Indoor' 3 'Home' 4 'Other'.

!TreeMap Data = NIBRS_2012 Vars = UCR_Cat V20061 Loc_Cat.
DATASET ACTIVATE Tree_Loc_Cat.

MATCH FILES FILE = *
  /FIRST = Flag_UCRType
  /BY UCR_Cat V20061.
DO IF Flag_UCRType = 0.
  DO REPEAT x = BL_x2 BL_y2 TR_x2 TR_y2.
    COMPUTE x = $SYSMIS.
  END REPEAT.
END IF.

*Calculating width, if under certain value not placing label.
MATCH FILES FILE = * /DROP UCR_Lab.
STRING UCR_Lab (A20).
IF (TR_x2 - BL_x2) >= 0.12 UCR_Lab = VALUELABEL(V20061).
EXECUTE.
 
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BL_x3 BL_y3 TR_x3 TR_y3 UCR_Cat UCR_Lab Loc_Cat
                BL_x2 BL_y2 TR_x2 TR_y2 MISSING=VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE TEMPLATE = "data\Labels_Poly.sgt".
BEGIN GPL
  PAGE: begin(scale(800px,600px))
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BL_x3=col(source(s), name("BL_x3"))
  DATA: BL_y3=col(source(s), name("BL_y3"))
  DATA: TR_x3=col(source(s), name("TR_x3"))
  DATA: TR_y3=col(source(s), name("TR_y3"))
  DATA: BL_x2=col(source(s), name("BL_x2"))
  DATA: BL_y2=col(source(s), name("BL_y2"))
  DATA: TR_x2=col(source(s), name("TR_x2"))
  DATA: TR_y2=col(source(s), name("TR_y2"))
  DATA: UCR_Cat=col(source(s), name("UCR_Cat"), unit.category())
  DATA: UCR_Lab=col(source(s), name("UCR_Lab"), unit.category())
  DATA: Loc_Cat=col(source(s), name("Loc_Cat"))
  TRANS: casenum = index()
  SCALE: linear(aesthetic(aesthetic.color.saturation.interior), aestheticMaximum(color.saturation."1"), 
         aestheticMinimum(color.saturation."0.4"))
  GUIDE: legend(aesthetic(aesthetic.color.interior), null())
  GUIDE: legend(aesthetic(aesthetic.color.saturation.interior), null())
  GUIDE: axis(dim(1), null())
  GUIDE: axis(dim(2), null())  
  ELEMENT: polygon(position(link.hull((BL_x3 + TR_x3)*(BL_y3 + TR_y3))), 
                   color.interior(UCR_Cat), split(casenum), transparency.exterior(transparency."1"),
                   color.saturation.interior(Loc_Cat))
  ELEMENT: polygon(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))),
                   transparency.exterior(transparency."1")), transparency.interior(transparency."1"),
                   label(UCR_Lab), split(casenum))
  ELEMENT: edge(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))), size(size."3"), split(casenum))
  PAGE: end()
END GPL.

The saturation for locations types goes from lightest to darkest: Outdoor, Indoor, Home, Other. Instead of randomly allocating the saturation to distinguish between the location types furthest down the hierarchy, I can map the saturation to another category. Here I map it to whether someone was arrested for the proportion of offenses.

*Adding in proportion of arrests.
DATASET ACTIVATE NIBRS_2012.
COMPUTE Arrest = (RECSARR > 0).
DATASET DECLARE ArrestProp.
AGGREGATE OUTFILE='ArrestProp'
  /BREAK UCR_Cat V20061 Loc_Cat
  /ArrestProp = MEAN(Arrest).
DATASET ACTIVATE Tree_Loc_Cat.
MATCH FILES FILE = *
  /TABLE = 'ArrestProp'
  /BY UCR_Cat V20061 Loc_Cat.
DATASET CLOSE ArrestProp.


*Now mapping arrest proportion to saturation.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=BL_x3 BL_y3 TR_x3 TR_y3 UCR_Cat UCR_Lab Loc_Cat ArrestProp
                BL_x2 BL_y2 TR_x2 TR_y2 MISSING=VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE TEMPLATE = "data\Labels_Poly.sgt".
BEGIN GPL
  PAGE: begin(scale(800px,600px))
  SOURCE: s=userSource(id("graphdataset"))
  DATA: BL_x3=col(source(s), name("BL_x3"))
  DATA: BL_y3=col(source(s), name("BL_y3"))
  DATA: TR_x3=col(source(s), name("TR_x3"))
  DATA: TR_y3=col(source(s), name("TR_y3"))
  DATA: BL_x2=col(source(s), name("BL_x2"))
  DATA: BL_y2=col(source(s), name("BL_y2"))
  DATA: TR_x2=col(source(s), name("TR_x2"))
  DATA: TR_y2=col(source(s), name("TR_y2"))
  DATA: UCR_Cat=col(source(s), name("UCR_Cat"), unit.category())
  DATA: UCR_Lab=col(source(s), name("UCR_Lab"), unit.category())
  DATA: Loc_Cat=col(source(s), name("Loc_Cat"))
  DATA: ArrestProp=col(source(s), name("ArrestProp"))
  TRANS: casenum = index()
  SCALE: linear(aesthetic(aesthetic.color.saturation.interior), aestheticMaximum(color.saturation."1"), 
         aestheticMinimum(color.saturation."0.4"))
  GUIDE: legend(aesthetic(aesthetic.color.interior), null())
  GUIDE: legend(aesthetic(aesthetic.color.saturation.interior), null())
  GUIDE: axis(dim(1), null())
  GUIDE: axis(dim(2), null())  
  ELEMENT: polygon(position(link.hull((BL_x3 + TR_x3)*(BL_y3 + TR_y3))), 
                   color.interior(UCR_Cat), split(casenum), transparency.exterior(transparency."1"),
                   color.saturation.interior(ArrestProp))
  ELEMENT: polygon(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))),
                   transparency.exterior(transparency."1")), transparency.interior(transparency."1"),
                   label(UCR_Lab), split(casenum))
  ELEMENT: edge(position(link.hull((BL_x2 + TR_x2)*(BL_y2 + TR_y2))), size(size."3"), split(casenum))
  PAGE: end()
END GPL.

This ends up being pretty boring though, there does not appear to be much variation within the location types for arrest rates. For here with widely varying category sizes I would likely want to do a model based approach and shrink the extreme proportions in the smaller categories, but that is a challenge for another blog post! (Also the sizes of the categories naturally de-emphasizes the small areas.)

One of the other things I was experimenting with was the use of svg gradients via the chart template, (see Squarified Treemaps (Bruls et al., 2000) for a motivating example) but I was unable to figure out the chart template xml needed to have the polygons drawn with gradients. (I had saved a few templates from V20 that had example gradients in them, and I’ve gotten them to work for bar graphs.) Also I attempted to export this with tooltips, but the tool tips were derived variables from the polygons, so I’m not quite sure how to cajole SPSS to give the tool tips I want.

This is not the best use of treemaps though, and I will have to write a post showing how small multiples of bar graphs can be just as effective as these examples. Shneiderman intended these to be an interactive application in which you could see the forest and then drill down into smaller subsets for exploration. Comparing areas across categories in this example, e.g. comparing the proportion of crimes occurring at home in assaults versus robberies, is very difficult to accomplish in the treemap. I would say that they are slightly more aesthetically pleasing than the wooden Charlie Brown xmas tree I built for my tiny apartment though.

Happy Holidays!

1 Comment
by Andy Wheeler on December 23, 2014  •  Permalink
Posted in Data Visualization, Macro, NIBRS, SPSS
Tagged ,

Posted by Andy Wheeler on December 23, 2014

https://andrewpwheeler.com/2014/12/23/treemaps-in-spss/

Repeating Charts in SPSS for unique IDs

The title is probably not that clear, but I’ve seen this request a few times and have used this trick in one my projects, so figured it would be a worthwhile topic to illustrate. So the problem is you have a background distribution, and you want to tailor a set of individual charts showing the unique individuals score against the background distribution. See two examples (1,2) of this question. In the first link I showed how one can do this by artificially duplicating the data in a specific way using VARSTOCASES and then using SPLIT FILE to generate the separate charts. Here I will show a python based solution that does not require duplicating the data.

So first we will start off with a set of fake student scores, 20 students with 5 scores each.

*Create some fake data, student test scores.
SET SEED 10.
INPUT PROGRAM.
STRING Student (A1).
LOOP #i = 1 TO 5.
  LOOP #j = 1 TO 20.
    COMPUTE Student = STRING(#j+64,PIB).
    COMPUTE Score = RND(RV.NORMAL(100,10)).
    END CASE.
  END LOOP.
END LOOP.
END FILE.
END INPUT PROGRAM.
DATASET NAME Student_Scores.
FORMATS Score (F3.0).
EXECUTE.

Now the students are listed as strings, but here I am going to use AUTORECODE to automatically turn the strings into number variables, and more importantly for what follows create a set of value labels corresponding to those unique strings.

*Use Auto-recode to make the variables 1 to N.
AUTORECODE VARIABLES = Student /INTO Student_N.
FORMATS Student_N (F6.0).

Now the workflow I want to do is to make a set of charts with the background a boxplot for the whole class, and then the individual students scores as foreground dots. To do this I will make a second set of scores that are missing for everyone except that one particular student, the specify MISSING=VARIABLEWISE on the GGRAPH command, and then superimpose Score2 over the boxplot of Score.

*Example of Individual chart.
NUMERIC flag (F1.0) Score2 (F3.0).

DO IF Student_N = 1.
  COMPUTE Score2 = Score.
  COMPUTE flag = 1.
ELSE.
  COMPUTE Score2 = $SYSMIS.
  COMPUTE flag = 0.
END IF.

GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Score Score2 flag MISSING = VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Score=col(source(s), name("Score"))
  DATA: Score2=col(source(s), name("Score2"))
  COORD: rect(dim(1), transpose())
  GUIDE: axis(dim(1), label("Score"))
  GUIDE: legend(aesthetic(aesthetic.visible), null())
  GUIDE: text.title(label("Student: A"))
  ELEMENT: schema(position(bin.quantile.letter(Score)), color.interior(color.grey))
  ELEMENT: point.dodge.symmetric(position(bin.dot(Score2)), color.interior(color.red))
END GPL.
*cleaing up temp variables.
MATCH FILES FILE = * /DROP flag Score2.

There are other ways to do this, like using the visible option in GPL aesthetics, but I don’t do that here because they still exist in the chart but simply aren’t shown. This causes problems with the dodging, and if you sent the chart in vector format the information would still be contained in the chart (e.g. if you need to aggregate the background data to be obfuscated for confidentiality reasons you don’t want it in the chart even if it is invisible). Here even the outlier dots in the boxplot are potentially disseminating confidential information, but for simplicity I don’t worry about that here (my syntax at the developerworks forum showed how you can build your own boxplot without having the points, it would be nice to have a no points option for the schema element).

So now the problem is looping through all of the individual students and generating a chart for each one. That is where the AUTORECODE comes in handy. I can grab all of the value labels from the SPSS dictionary and place them in a Python dictionary.

*Python to grab the different students.
BEGIN PROGRAM Python.
import spss
spss.StartDataStep()
datasetObj = spss.Dataset()
StudentLab = datasetObj.varlist['Student_N'].valueLabels
print StudentLab #this is a dictionary of all the unique students
spss.EndDataStep()
END PROGRAM.

Now with the StudentLab Python dictionary I can loop over the dictionary and submit the SPSS syntax for each unique student (using spss.Submit) using string substitutions. I first create the variables and set there formats outside of the loop (the chart inherits the formats). Then I just set several aesthetics of the charts so they are the same for every chart, e.g. the scale goes between 60 and 150, and the size of the superimposed points is 12.

*Now loop through the students.
OUTPUT CLOSE ALL.
BEGIN PROGRAM Python.
spss.Submit("NUMERIC flag (F1.0) Score2 (F3.0).")
for val, lab in StudentLab.data.iteritems():
  spss.Submit("""*Individual score chart.
DO IF Student_N = %d.
  COMPUTE Score2 = Score.
  COMPUTE flag = 1.
ELSE.
  COMPUTE Score2 = $SYSMIS.
  COMPUTE flag = 0.
END IF.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Score Score2 flag MISSING = VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Score=col(source(s), name("Score"))
  DATA: Score2=col(source(s), name("Score2"))
  DATA: id=col(source(s), name("$CASENUM"), unit.category())
  DATA: flag=col(source(s), name("flag"), unit.category())
  COORD: rect(dim(1), transpose())
  GUIDE: axis(dim(1), label("Score"), delta(10), start(60))
  GUIDE: text.title(label("Student: %s"))
  GUIDE: legend(aesthetic(aesthetic.visible), null())
  SCALE: linear(dim(1), min(60), max(150))
  ELEMENT: schema(position(bin.quantile.letter(Score)), color.interior(color.grey))
  ELEMENT: point.dodge.symmetric(position(bin.dot(Score2)), color.interior(color.red),
           size(size."12"))
END GPL.
""" %(val,lab))
END PROGRAM.

I wanted to export these charts in the loop with the students names, using something like:

SpssOutputDoc.SelectLastOutput() #grab last output
SpssOutputDoc.ExportCharts(SpssClient.SpssExportSubset.SpssSelected, path + lab, SpssClient.ChartExportFormat.png)

but what happens with this is that it is always one behind (e.g. the first chart is selected in the second loop iteration). So what I did was to stuff all of the charts within a list and then loop over that list, select the chart, and then export it using SpssOutputDoc.ExportCharts (another option would be to use EXPORT OUTPUT and then either delete the output in-between charts or clear it, I wish OMS could export only charts). This would be more annoying with multiple individual charts, and could likely be made more concise, but here it is.

*Now exporting the individual charts.
BEGIN PROGRAM Python.
import SpssClient
SpssClient.StartClient()
SpssOutputDoc = SpssClient.GetDesignatedOutputDoc()

#creating a list of all the charts
OutputItems = SpssOutputDoc.GetOutputItems()
Charts = []
for index in range(OutputItems.Size()):
  OutputItem = OutputItems.GetItemAt(index)
  if OutputItem.GetType() == SpssClient.OutputItemType.CHART:
    Charts.append(OutputItem)

labList = []
for val, lab in StudentLab.data.iteritems():
  labList.append(lab)

path = "C:/Users/andrew.wheeler/Dropbox/Documents/BLOG/RepeatingCharts/"

for chart,lab in zip(Charts,labList):
  SpssOutputDoc.ClearSelection() #clear prior selections
  chart.SetSelected(True) #select chart
  #export chart
  SpssOutputDoc.ExportCharts(SpssClient.SpssExportSubset.SpssSelected, path + lab, SpssClient.ChartExportFormat.png)
END PROGRAM.

Here is a screen shot of the resulting images in my folder.

So this will export the charts to PNG format with the image name the same as the students in the file (so the name needs to be in a format appropriate to save a file name). Annoyingly SPSS appends 1 to the end of all charts, even if it is only exporting one chart. Here is an example of the student G’s chart.

Eventually I will figure out how to send emails via Python, and this would be a good tool for individualized report cards for a class. Here is a copy of the full syntax to more easily run on your local machine (just replace path with a location on your local machine).

4 Comments
by Andy Wheeler on December 19, 2014  •  Permalink
Posted in Python, SPSS
Tagged , , ,

Posted by Andy Wheeler on December 19, 2014

https://andrewpwheeler.com/2014/12/19/repeating-charts-in-spss-for-unique-ids/

Solving problems as a metaphor for scientific writing

One analogy I hear in academics describing the process of writing a literature review is identifying the gaps in prior literature(s). I was reading Helping doctoral students write: Pedagogies for supervision recently, and Kamler & Thomson used this same analogy in describing the process of writing a literature review for a dissertation (although it is generally the same for shorter articles or books). Similar terminology Kamler & Thomson describe are blank spots and blind spots (see page 45). In that same chapter since Kamler & Thomson suggest the use of appropriate metaphors in describing the work of writing a literature review, I figured a critique of this one to be apropos.

I do not think the analogy is completely off base — but I do not like it as it does not jive with my personal experience of how I go about writing an article or thinking about research more generally. The first reason I do not like this terminology is that it has negative connotations for prior research. I think of building knowledge as a more cumulative endeavour as opposed to filling in between the lines of prior research.

For an analogy, say a researcher is attempting to improve the fuel efficiency of small combustible engines. It is likely they take mostly prior engineering knowledge about combustible engines and provide some modifications to slightly improve the design. Filling a gap implies to me an explicit design flaw in prior engines, when in reality it is more likely the researcher brings new knowledge to improve the design, and only in the context of the new research is the old design potentially described as inefficient. A social science example may be evaluating the costs and benefits to a particular policy in place by a public institution. The policy may be evidence based, and so an evaluation of the policy provides new information to that agency of whether it works as intended, or more general scientific knowledge about applying that policy in a real world setting. Neither seem to me filling in a gap, more so contributing and/or refining a set of knowledge already established.

I like the metaphor of the accumulation of knowledge, like a pyramid one brick at a time, better in terms of describing what I do when I write a literature review as opposed to identifying gaps. A convenient format for a literature review is to take a historical walk through the literature, and let the chronological order of previous findings be the guide for how you write the lit. review. But that metaphor is not sufficient to me either, as it implies a very linear structure, whereas prior research strikes me as more sphere-like — there is a base to which you add but the direction of the current research is not limited by the trajectory of the prior work. (A more accurate physical analogy may be an irregular growth of cells — they may meander in any particular direction but they always need to be connected to the prior work.) The scientific writer imposes a linear structure when describing prior work, but in reality the prior literatures are not that focused on whatever particular problem the current article is trying to address.

That is why I like the simple metaphor of identifying and solving a problem as a descriptor of what I do when I write a literature review – or even more broadly about describing the decisions I make in my research agenda. There are several reasons I prefer this analogy to either the accumulation of knowledge or identifying gaps. Identifying gaps implies you can read the prior literature and the gaps will be obvious — this is not the case. The prior literature is written in a particular context – the authors cannot anticipate future conditions or how that work will potentially be applied in the future. The gap does not exist in the current or prior literatures, you as a writer/researcher make the gap. I prefer problem solving as opposed to the accumulation of knowledge because it implies the focused nature of the endeavour. You do not simply write a paper to add a linear line of prior knowledge, you use that prior knowledge to solve a particular problem you have in your current context. It is your job as a researcher to basically say how the prior knowledge helps to solve that problem, and then advance the current knowledge to solve your particular problem. (This focus on giving the writer agency seems to be in line with most of Kamler & Thomson’s advice as well.)

This is how Popper described how knowledge actually accumulates — people have problems and they try to learn how to solve them. There is no prior divine truth to which future knowledge is added. We simply have problems, and some research may show a better solution to that problem than prior knowledge (be it whether the prior knowledge is well established or simply folklore). The analogy is not perfect, as many researchers would say they do not solve problems but are simply describe reality, but is a frame of reference I find useful to describe how I approach writing, describe my research, and in particular how I approach consuming the prior literature. It shows how I take the prior work and apply it to my interest, I am not a passive reader when trying to synthesize prior work.

3 Comments
by Andy Wheeler on December 12, 2014  •  Permalink
Posted in scholarly, writing
Tagged

Posted by Andy Wheeler on December 12, 2014

https://andrewpwheeler.com/2014/12/12/solving-problems-as-a-metaphor-for-scientific-writing/

Musings on Comments

I recently posted a comment policy. I do not get that many comments now, but I did delete a comment recently asking for help on a code sample, so figured it would be worth elaborating on.

Comments are great, and I hope to get more, but with my participation on the stack exchange sites (and commenting on other blogs) I definitely see the need to take active moderation. This is not a big deal for the site so far (I rarely post anything controversial) but is really necessary for any blog generating a lot of comments.

My position is not quite extreme as Ed Tufte, e.g. I don’t plan on deleting a comment if I don’t like the content enough, but I will definitely delete off-topic comments and anything I find offensive. My position is more in line with Jeff Atwood’s thoughts, who discusses the topic quite a bit on his coding horror blog (see here for one example).

Basically the comments take curation, just like any site or wiki. Comments without moderation in any substantive amount (e.g. YouTube, many news articles) are simply not worth reading. The same moderation is what makes the stack exchange sites so much better than email list-serves, and the lack of moderation is what makes some MOOC forums so chaotic.

Leave a comment
by Andy Wheeler on December 7, 2014  •  Permalink
Posted in Meta
Tagged

Posted by Andy Wheeler on December 7, 2014

https://andrewpwheeler.com/2014/12/07/musings-on-comments/

Automating tasks in SPSS using production jobs

For tasks that take a long time, or ones I want done on a regular basis, I typically have the computer do the work while I am away. Such example tasks I have set up before are:

  • querying large databases and dumping the results into flat files (querying large tables may take an hour or longer)
  • conducting statistical analysis that takes a long time to converge
  • generating automated graphs and statistics

The SPSS facility to accomplish these are production jobs, and I will briefly detail how to set up a production job and then run the job from the command line with a simple example.

So first to set up a production job go to Utilities -> Production Facility in the menu bar. (Note you can open the screen shots larger in a separate window.)

Next you will be presented with the screen below. To specify the syntax file(s) that the production job will run, click the New button.

After you click the New button, the green plus sign in the Syntax files section will be active, and then you can browse to your sps file. Here you can see I selected a file named GenerateChart.sps in a particular directory on my C drive. You can specify the job to run multiple syntax files, but here I only choose one.

Next navigate to the Output section of the window. Here you need to choose where to save the SPSS output. Here I choose to save it in the same directory under the name Output. I choose the output format to be plain text. This ends up being the same output as if you ran the syntax interactively and then used EXPORT OUTPUT.

I could have exported the charts in the syntax directly by using EXPORT OUTPUT, but you can have the production facility do that as well. If you click on the Options button in the Output section a new dialogue will appear that lets you choose to save the charts if you want. Here I save them as png files.

Production jobs also have the capability to create user input variables directly in the syntax, using the form @VariableName in the syntax. This is what the section Run time variables deals with. These are nice if you have a set of syntax and want to input some arbitrary information, as when you run the production job a GUI pops up asking for the input, but I don’t illustrate that functionality here.

Below is the specific set of syntax that grabs a csv file, swdata.csv, calculates a moving median for each chat room, and makes some time series charts. The csv file is a set of scrapped chat data from the Cross Validated and R chat rooms via Scraperwiki (more details here). It aggregates the number of monologue tags (a pretty good indicator of the number of posts in the room) per day, so is an estimate of the chat activity.

*Where the data is located.
FILE HANDLE data 
  /NAME = "C:\Users\andrew.wheeler\Dropbox\Documents\BLOG\ProductionJob".
DATA LIST LIST (",") FILE = "data\swdata.csv" SKIP = 1 
  /Date (SDATE10) Mono (F4.0) Baseroom (A100).
DATASET NAME Chats.

*Calculate moving median.
AUTORECODE VARIABLES = Baseroom /INTO BaseN.
SORT CASES BY BaseN Date.
SPLIT FILE BY BaseN.
CREATE MovMed = RMED(Mono 5).
FORMATS MovMed (F4.0) Date (MOYR6).

*Make charts.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Date Mono MovMed 
   MISSING=VARIABLEWISE
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Date=col(source(s), name("Date"))
  DATA: Mono=col(source(s), name("Mono"))
  DATA: MovMed=col(source(s), name("MovMed"))
  GUIDE: axis(dim(1))
  GUIDE: axis(dim(2), label("Mono Tags"))
  ELEMENT: line(position(Date*Mono), color(color.grey), 
           transparency(transparency."0.5"), size(size."1"))
  ELEMENT: line(position(Date*MovMed), color(color.red), 
           transparency(transparency."0.4"), size(size."1"))
END GPL.

Now I am interested in running this set of syntax automatically. The details will change depending on your operating system, but on my windows machine the easiest way to do this is to create a bat file that specifies the commands. Now I named the production job ChatRoom_Dialogue.spj, and to run this job I filled in the bat file with the text:

REM delete old csv file and download new one
del swdata.csv
wget "http://goo.gl/mxyRI7" --no-check-certificate
REM this runs the SPSS syntax
"C:\Program Files\IBM\SPSS\Statistics\22\stats.exe"  "C:\Users\andrew.wheeler\Dropbox\Documents\BLOG\ProductionJob\ChatRoom_Dialogue.spj" -production silent

Here I downloaded the wget utility to grab the csv file. (Note REM is to comment lines.) The bat file treats where ever it is located at as the directory for the commands, so I first use del to delete the older csv file, and then grab the new csv file from the listed url and it automatically saves the file in the folder where the bat file is located. Then I call the SPSS syntax by starting stats.exe and then calling the spj production job file. I use the switches -production silent so I am not prompted for any user input values to insert into the syntax. If you had stats.exe as a windows system path you wouldn’t need to worry about using the fully quoted strings, but I typically don’t rely on that (unless the program automatically adds it). Note that running the fully quoted string for stats.exe makes the windows command directory go to there, so you need to then fully quote the spj files path. Note you could call the first two commands directly within SPSS using the HOST command, but being able to chain multiple commands together makes running them in the bat file directly a bit more flexible.

So now you can simply double click the bat file and it will download the new data and create two graphs. To automate the job you can use the Windows task scheduler to make the bat file run at a particular time. Here is the bundled up files to run on your own (you just need to change the files paths in the sps and the bat file to wherever you want to run the script).

Here are the two graphs the production job creates. The first is the Cross Validated chat room, and the second is the R stackoverflow chat room.

I planned on writing a blog post for the CV blog awhile ago about these trends, so if I ever get to it these are teasers.

9 Comments
by Andy Wheeler on December 3, 2014  •  Permalink
Posted in SPSS
Tagged

Posted by Andy Wheeler on December 3, 2014

https://andrewpwheeler.com/2014/12/03/automating-tasks-in-spss-using-production-jobs/

Using the Google Distance API in SPSS – plus some EDA of travel time versus geographic distance

The other day I had a conversation with a colleague about calculating travel time distances and comparing them to actual geographic distances (aka as the crow flies). Being unfamiliar with the Network add-on in ArcGIS I figured I would take a stab at this task with the Google Distance API. Being lazy, I’m not going to explain the code, but in a nutshell works basically the same way as my prior code samples for the Google places API. The main difference is that this code will only return one result per record in the original file.

BEGIN PROGRAM Python.
import urllib, json

#This parses the returned json to pull out the distance in meters and
#duration in seconds, [None,None] is returned is status is not OK
def ExtJsonDist(place):
  if place['rows'][0]['elements'][0]['status'] == 'OK':
    meters = place['rows'][0]['elements'][0]['distance']['value']
    seconds = place['rows'][0]['elements'][0]['duration']['value']
  else:
    meters,seconds = None,None
  return [meters,seconds]

#Takes a set of lon-lat coordinates for origin and destination,
#plus your API key and returns the json from the distance API
def GoogDist(OriginX,OriginY,DestinationX,DestinationY,key):
  MyUrl = ('https://maps.googleapis.com/maps/api/distancematrix/json'
           '?origins=%s,%s'
           '&destinations=%s,%s'
           '&key=%s') % (OriginY,OriginX,DestinationY,DestinationX,key)
  response = urllib.urlopen(MyUrl)
  jsonRaw = response.read()
  jsonData = json.loads(jsonRaw)
  data = ExtJsonDist(jsonData)
  return data
END PROGRAM.

So because for each pair of origin and destinations this only returns one result, we can use this function in SPSSINC TRANS to return the distance in meters and the travel time in seconds without having to worry about any other data manipulations in python. The only additional item we need besides the origin and destination latitude and longitude are your Google API key in a seperate string variable. So if you had the OD coordinates in the fields Ox,Oy,Dx,Dy for origin longitude, origin latitude etc. the code would simply be:

STRING MyKey (A100).
COMPUTE MyKey = '!!!!!!!YOUR KEY HERE!!!!!!!!!!!!!'.
EXECUTE.

SPSSINC TRANS RESULT=Meters Seconds TYPE=0 0 
/FORMULA GoogDist(OriginX=Ox,OriginY=Oy,DestinationX=Dx,DestinationY=Dy,key=MyKey).

Note the Google distance API has a limit of 2,500 queries per day, and unlike the places API can not be upped by providing verification (unfortunately).

The context the colleague was asking was for a project about prison visitation, for some background see a report by Jacquelyn Greene at the New York State DCJS, and I saw recently Joshua Cochran plus a few other of the Florida State folks published a paper about prisoner visitation in Florida. So I figured a good test would be calculating the correlation between travel distance and geographic distances between all of the zip codes in New York State to one particular prison.

I chose to calculate the distances between the centroid of zip code areas and Attica State prison, which is in between Rochester and Buffalo in the westernmost part of New York state. FYI zip code areas are not well defined, so don’t ask me how exactly the ones I used here are calculated, but I got them from the New York State GIS clearinghouse, and they were from 2009.

So as long as you have the prior python function GoogDist defined, here is a set of brief syntax to grab the zip code data and calculate the travel time and travel distance. This does take a few minutes, but I never had a problem with the 100 queries per 1 minute suggestion by Google in my tests. Their are 2,332 zip code areas in New York State, so beware this about uses up your limit for the day (and you have no second chances)! This took me about 8 minutes to calculate.

*Grab the online data.
SPSSINC GETURI DATA
URI="https://dl.dropboxusercontent.com/u/3385251/NewYork_ZipCentroids.sav"
FILETYPE=SAV DATASET=NY_Zips.

*Travel distance to Attica.
COMPUTE Dx = -78.276205.
COMPUTE Dy = 42.850721.

STRING MyKey (A100).
COMPUTE MyKey = '!!!!!!!YOUR KEY HERE!!!!!!!!!!!!!'.
EXECUTE.

SPSSINC TRANS RESULT=Meters Seconds TYPE=0 0 
/FORMULA GoogDist(OriginX=LongCent,OriginY=LatCent,DestinationX=Dx,DestinationY=Dy,key=MyKey).

We can also calculate the euclidean "crows flies" distance via the extendedTransforms python code. This returns the distance miles, and so the following code converts the two distances to kilometers and the time to minutes.

*As the crow flies distance.
SPSSINC TRANS RESULT=MilesCrow TYPE=0
/FORMULA extendedTransforms.ellipseDist(lat1=LatCent,lon1=LongCent,lat2=Dy,lon2=Dx,inradians=False).

*Convert to meters. 
COMPUTE KMCrow = (MilesCrow*1609.34)/1000.
COMPUTE KMTrav = Meters/1000.
COMPUTE Minutes = Seconds/60.
FORMATS KMCrow KMTrav Minutes (F6.0).

Now, part of my suggestion was actually that calculating travel times is not necessary, because they will be highly correlated with each other. Here is the scatterplot matrix of the three measures, travel distance, geographic distance, and travel time. The inter-item correlations are all around .99.

GGRAPH 
  /GRAPHDATASET NAME="graphdataset" VARIABLES=KMCrow KMTrav Minutes 
  /GRAPHSPEC SOURCE=INLINE. 
BEGIN GPL 
  SOURCE: s=userSource(id("graphdataset")) 
  DATA: KMCrow=col(source(s), name("KMCrow")) 
  DATA: KMTrav=col(source(s), name("KMTrav")) 
  DATA: Minutes=col(source(s), name("Minutes")) 
  GUIDE: axis(dim(1.1), ticks(null())) 
  GUIDE: axis(dim(2.1), ticks(null())) 
  GUIDE: axis(dim(1), gap(0px)) 
  GUIDE: axis(dim(2), gap(0px)) 
  TRANS: KMCrow_label = eval("KMCrow") 
  TRANS: KMTrav_label = eval("KMTrav") 
  TRANS: Minutes_label = eval("Minutes") 
  ELEMENT: point(position((KMCrow/KMCrow_label+KMTrav/KMTrav_label+Minutes/Minutes_label)*
                (KMCrow/KMCrow_label+KMTrav/KMTrav_label+Minutes/Minutes_label)),
                 size(size."2"), transparency.exterior(transparency."0.8"))  
END GPL.
CORRELATIONS VARIABLES= KMCrow KMTrav Minutes.

I expected that the error would get larger for larger travel and geographic distances, so to investigate this a simple graphical check is to estimate the difference between the two measures on the Y axis and the mean of the two measures on the X axis. Depending on who you ask, this is a Tukey mean difference plot or a Bland-Altman plot. Generally when comparing the scatterplot matrices it is easier to see the spread when you detilt the plot (using Tukey’s terminology), and calculating the differences is one way to do the detilting.

Here I calculate Dif = TravelDistance - GeoDistance, as I know the travel distance will always be larger than the geographic distance. For simplicity I just plot the geographic distance on the x axis instead of the mean of the two measures.

*Tukey mean difference chart.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=KMTrav KMCrow MISSING=LISTWISE REPORTMISSING=NO
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: KMTrav=col(source(s), name("KMTrav"))
  DATA: KMCrow=col(source(s), name("KMCrow"))
  TRANS: Dif = eval(KMTrav - KMCrow)
  GUIDE: axis(dim(2), label("Travel - Crows"))
  GUIDE: axis(dim(1), label("Crows Distance (in Kilometers)"))
  ELEMENT: point(position(KMCrow*Dif))
END GPL.

This shows three particular things:

  1. It appears to be a mostly mixture of two separate linear regressions
  2. Within each mixture the measurement error is close to a constant multiple of the geographic distance
  3. There are some outliers as fingers of large travel distances extending from the point cloud.

Some more EDA shows that the mixture is reflective of being close to Interstate 90 – those cities (like Albany and Syracuse) nearby the highway have a shorter travel time. Here what I did was estimate the linear regression for the prior plot and then color the residuals. Then I made a side-by-side set of the latitude-longitude coordinates next to the same scatterplot (colored). I can’t tell from this plot, but some of the high outliers appears in a cluster in downstate, maybe in the Catskills. But there are a few other of the high outliers shown around the state.

*Note this is the same as estimating regression on differences. 
*see http://stats.stackexchange.com/a/15759/1036. 
REGRESSION
  /MISSING LISTWISE
  /STATISTICS COEFF OUTS R ANOVA
  /CRITERIA=PIN(.05) POUT(.10)
  /NOORIGIN 
  /DEPENDENT KMTrav
  /METHOD=ENTER KMCrow
  /SAVE RESID(Resid1).

*Hmm, we have a mixture, lets see what explains that.
GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=LongCent LatCent Resid1 KMTrav KMCrow
    MISSING=LISTWISE REPORTMISSING=NO
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  PAGE: begin(scale(500px,800px))
  SOURCE: s=userSource(id("graphdataset"))
  DATA: LongCent=col(source(s), name("LongCent"))
  DATA: LatCent=col(source(s), name("LatCent"))
  DATA: Resid1=col(source(s), name("Resid1"))
  DATA: KMTrav=col(source(s), name("KMTrav"))
  DATA: KMCrow=col(source(s), name("KMCrow"))
  TRANS: Dif = eval(KMTrav - KMCrow)
  GRAPH: begin(origin(15%, 5%), scale(81%, 40%))
  GUIDE: axis(dim(1), null())
  GUIDE: axis(dim(2), null())
  GUIDE: legend(aesthetic(aesthetic.color.interior), null())
  SCALE: linear(aesthetic(aesthetic.color), aestheticMinimum(color.lightgrey), aestheticMaximum(color.black))
  ELEMENT: point(position(LongCent*LatCent), color.interior(Resid1), size(size."5"), transparency.exterior(transparency."0.7"))
  GRAPH: end()
  GRAPH: begin(origin(15%, 50%), scale(81%, 40%))
  GUIDE: axis(dim(2), label("Travel - Crows"))
  GUIDE: axis(dim(1), label("Crows Distance (in Kilometers)"))
  GUIDE: legend(aesthetic(aesthetic.color.interior), null())
  SCALE: linear(aesthetic(aesthetic.color), aestheticMinimum(color.lightgrey), aestheticMaximum(color.black))
  ELEMENT: point(position(KMCrow*Dif), color.interior(Resid1), size(size."5"), transparency.exterior(transparency."0.7"))
  GRAPH: end()
  PAGE: end()
END GPL.

The linear regression gives a rough estimate for the relationship between travel distance and geographic distance in this sample that is about:

Travel Distance in = -4.7 + 1.3*Geographic Distance

A better model would include an interaction between distance to I-90 (and then maybe a term for being in the mountains), but again I am lazy! Obviously the negative intercept doesn’t make physical sense, so you really only want to use this for geographic distances of say 50 kilometers or larger, else it will likely be an underestimate. The opposite is true if you are close to I-90, this formula is likely to be an overestimate.

The same exercise for the travel time in minutes gives the equation Travel Time in Minutes = 9 + 0.75*(Geographic Distance in Kilometers):

*Minutes as a function of distance.
REGRESSION
  /MISSING LISTWISE
  /STATISTICS COEFF OUTS R ANOVA
  /CRITERIA=PIN(.05) POUT(.10)
  /NOORIGIN 
  /DEPENDENT Minutes
  /METHOD=ENTER KMCrow
  /SAVE RESID(MinResid).

COMPUTE AbsResid = ABS(MinResid).
COMPUTE DirResid = MinResid/AbsResid.

GGRAPH
  /GRAPHDATASET NAME="graphdataset" VARIABLES=Minutes KMCrow AbsResid DirResid
  /GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
  SOURCE: s=userSource(id("graphdataset"))
  DATA: Minutes=col(source(s), name("Minutes"))
  DATA: KMCrow=col(source(s), name("KMCrow"))
  DATA: AbsResid=col(source(s), name("AbsResid"))
  DATA: DirResid=col(source(s), name("DirResid"), unit.category())
  TRANS: Dif = eval(KMTrav - KMCrow)
  GUIDE: axis(dim(2), label("Travel Minutes"))
  GUIDE: axis(dim(1), label("Crows Distance (in Kilometers)"))
  GUIDE: legend(aesthetic(aesthetic.color.interior), null())
  GUIDE: legend(aesthetic(aesthetic.transparency.interior), null())
  GUIDE: legend(aesthetic(aesthetic.size), null())
  SCALE: linear(aesthetic(aesthetic.size), aestheticMinimum(size."3"), aestheticMaximum(size."13"))
  SCALE: linear(aesthetic(aesthetic.transparency), aestheticMinimum(transparency."0.3"), aestheticMaximum(transparency."0.9"), reverse())
  ELEMENT: point(position(KMCrow*Minutes), color.interior(DirResid), transparency.interior(AbsResid),
                 size(AbsResid), transparency.exterior(transparency."1"))
  ELEMENT: line(position(smooth.linear(KMCrow*Minutes)))
END GPL.

Again the mixture appears, but the linear regression appears as a much closer fit between geographic distance and travel time.

So in both cases, at least in this sample, it appears it is not really necessary to calculate travel distance. One can make a pretty good guess as to the travel distance simply given the geographic distance. Or going the other way using Pennsylvania speak, if I say the distance between two locations is about 1 hour this would translate into about 68 kilometers (i.e. 42 miles).

6 Comments
by Andy Wheeler on November 19, 2014  •  Permalink
Posted in Data Visualization, Python, SPSS
Tagged , ,

Posted by Andy Wheeler on November 19, 2014

https://andrewpwheeler.com/2014/11/19/using-the-google-distance-api-in-spss-plus-some-eda-of-travel-time-versus-geographic-distance/

Big data problems for Criminal Justice

I am on the job market this year, and I have noticed a few academic jobs focused on big data (see this Penn State posting for one example). Because example data sets in criminal justice are not typical fodder for big data conversations, I figured I would talk abit about my experiences and illustrate the need for the types of skills needed to manipulate and analyze these big datasets.

As opposed to trying to further define the big data buzzword, I will simply talk about the actual size of data I have dealt with. Depending on the definition used, most large criminal justice datasets may be called medium sized data. That is you can load it in a database or statistical program (particularly those that do not load everything into RAM, like SPSS and SAS) and calculate different summary statistics and fit simple models. Were not talking about datasets that need custom big data solutions like Hadoop. The biggest single table I’ve personally worked with is a set of 25 million arrest histories (with around 150 variables). Using SPSS server to sort this dataset took less than a minute, using my local machine it took about 10 minutes. Nothing much to complain about there, and it is where the statistical programs that don’t load everything into memory shine.

To talk specifics, the police agency where I was an analyst at (Troy, NY) is a fairly small city with a population of around 50,000 people. They generated around 60,000 calls for service per year (this includes anytime someone calls 911, or police initiated interactions like a traffic stop). Every single one of these incidents generates a one to many relationship for multiple tables, and here is a sampling of those relationships; multiple free text description of the event and follow up investigations, people involved in the incident, offences committed, property stolen or damaged, persons arrested, property recovered or confiscated, drug and weapon contraband, vehicles involved, etc. Over the time period of 04-13 the incident narratives themselves are around 1 gigabyte, and the number of unique individuals and institutions in the "names" table was around 100,000. None of these tables alone would be considered big data, but when taking multiple years and having to conduct multiple table merges it turns into complicated medium size data pretty quickly.

I’m sure I’m not alone here working with police departments. In the past month I’ve had conversations with two individuals about corrections datasets that result in millions of records. Criminal justice organizations have been collecting data for along time, and given say 50,000 records per year it only takes 10 years to turn that into 500,000. When considering larger agencies (like statewide corrections or courts) the per year becomes even larger.

Most of the time summary statistics and fairly simple regression models are all researchers and analysts are interested in in criminal justice. The field is not heavily devoted to prediction, and certainly not to fitting complicated machine learning models. Many regression tasks can be estimated with data as large as 25 million records (given that the number of predictor variables tends to be small) and even if it didn’t sampling (or reducing the data to unique observations and weighting) is an obvious option. So for these types of simple needs just learning effective practices at manipulating datasets — such as SQL and best practices for conducting data manipulations in statistical packages is most of the education one needs. But these are still definitely needs that are not met in any social science curricula that I am aware. By fire is my only experience.

Two particular areas that turn little data into big data are spatial and network analysis, as one not only needs to consider the number of nodes but also the number of edges (or potential edges) in the system to calculate various measures. For example, in my dissertation I needed to conduct spatial lags of several variables (and this is needed in calculating measures such as Moran’s I). In matrix notation this typically involves calculating Wx, where W is an n by n spatial weights matrix. In my dissertation, n was 21,506, so not a large dataset, but W is then a 21,506^2 matrix. It can be held in memory, but good luck trying to calculate anything with it. Most of the spatial econometrics literature discusses how calculating W^-1 is problematic, let alone the simpler operation of Wx. So to do those calculations I needed to create custom code. I hope to be able to write a blog post on how it can be done at some point – but these blog posts aren’t earning me any brownie points to getting a job (let alone getting tenure in the future).

The other area that I believe needs to be developed in the social science related to medium data problems are custom visualization solutions. Data in social science typically has lots of noise to signal, and adding in 100,000 observations rarely makes things clearer. This is why I think visualization within the social sciences has potential to expand, as the majority of historical discussions are not extensible to our particular use applications in the social sciences.

So I’m excited by academia recognizing that big data is a problem and takes custom solutions in the social sciences. An environment where I can be reworded for taking on those big data tasks and partly focus on publishing software, as opposed to solely publish or perish, would help develop the field and have a more lasting impact on practical applications than journal articles. At least a place that acknowledges the need to develop curricula related to these data management tasks would be a good start. But I’m not sure I like the types of applications currently being pitched in the social sciences as big data problems, particularly the trivial applications of examining social networks like facebook or twitter, nor emphasis on big data tools like Hadoop that I don’t think are applicable to the social scientists toolset. But I’m certainly biased to think that applications in criminal justice have more practical implications than alot of contemporary social science research.

Leave a comment
by Andy Wheeler on November 11, 2014  •  Permalink
Posted in Criminal Justice, scholarly
Tagged , , ,

Posted by Andy Wheeler on November 11, 2014

https://andrewpwheeler.com/2014/11/11/big-data-problems-for-criminal-justice/

« Older Posts
Newer Posts »