Sorry about the long title! Previously I have blogged about how to use Deep Learning to generate an RTM like model variable selection and positive constraints. Deep learning frameworks often do not rely on variable selection like that though, they more often leverage hidden layers. For social scientists familiar with structural equation modelling, these hidden layers are very much akin to formative latent variables. (More traditionally folks use reflective latent variables in factor analysis, so the latent variable causes the observed measures. This is the obverse, the observed measures cause/define the latent variable, and we find the loadings that best predict some outcome further down the stream.)
In a nutshell, instead of the typical RTM way of picking the best variable to use, e.g. Alcohol Density < 100 meters OR Alcohol Density < 500 meters, it allows both to contribute to a latent variable, call it AlcoholDens, but allows those weights to vary. Then I see how well the AlcoholDens latent variable predicts crime. I will show later in the results that the loadings are often spread out among different density/distance measures in this sample, suggesting the approach just pick one is perhaps misguided.
I’ve posted the data and code to follow along here. There are two py files, 00_RTMHidden.py runs the main analysis, but dl_rtm_funcs.py has various functions used to build the deep learning model in pytorch. I am just going to hit some of the highlights instead of walking through bit by bit.
Some helper functions
First, last blog post I simply relied on using Poisson loss. This time, I took some effort to figure out my own loss function for the negative binomial model. Here I am using the NB2 form, and you can see I took the likelihood function from the Stata docs (they are a really great reference for various regression model info). To incorporate this into your deep learning model, you need to add a single parameter in your model, here I call it disp.
#Log likelihood taken from Stata docs, pg 11
#https://www.stata.com/manuals13/rnbreg.pdf
def nb2_loss(actual, log_pred, disp):
m = 1/disp.exp()
mu = log_pred.exp()
p = 1/(1 + disp.exp()*mu)
nll = torch.lgamma(m + actual) - torch.lgamma(actual+1) - torch.lgamma(m)
nll += m*torch.log(p) + actual*torch.log(1-p)
return -nll.mean()A second set of helper functions I will illustrate at the end of the post is evaluating the fit for Poisson/Negative Binomial models. I’ve discussed these metrics before, they are just a python rewrite of older SPSS code I made.
def pred_nb(mu, disp, int_y):
inv_disp = 1/disp
p1 = gamma(int_y + inv_disp) / ( factorial(int_y)*gamma(inv_disp) )
p2 = ( inv_disp / (inv_disp + mu) ) ** inv_disp
p3 = ( mu / (inv_disp + mu) ) ** int_y
pfin = p1*p2*p3
return pfin
def nb_fit(mu, obs, disp, max_y):
res = []
cum_fit = mu - mu
for i in range(max_y+1):
pred_fit = pred_nb(mu=mu, disp=disp, int_y=i)
pred_obs = (obs == i)
res.append( (str(i), pred_obs.mean(), pred_fit.mean(), pred_obs.sum(), pred_fit.sum()) )
cum_fit += pred_fit
fin_fit = 1 - cum_fit
fin_obs = (obs > max_y)
res.append( (str(max_y+1)+'+', fin_obs.mean(), fin_fit.mean(),
fin_obs.sum(), fin_fit.sum()) )
dat = pd.DataFrame(res, columns=['Int','Obs','Pred','ObsN','PredN'])
return datMain Analysis
Now onto the main analysis. Skipping the data loading (it is near copy-paste from my prior RTM Deep Learning post), here are the main guts to building and fitting the RTM model.
model = dl_rtm_funcs.RTM_hidden(gen_list=[alc_set,metro_set,c311_set],
gen_names=['AlcOutlets','MetroEntr','Dens311'])
optimizer = torch.optim.Adam(model.parameters(), lr=0.001) #1e-4
for t in range(5001):
#Forward pass
y_pred = model(comb_ten)
#Loss
loss_insample = dl_rtm_funcs.nb2_loss(y_ten, y_pred, model.dispersion)
optimizer.zero_grad()
loss_insample.backward() #retain_graph=True
optimizer.step()
if t % 100 == 0:
loss_out = dl_rtm_funcs.nb2_loss(out_ten, y_pred, model.dispersion)
print(f'iter {t}: loss in = {loss_insample.item():.5f}, loss out = {loss_out.item():.5f}')And in terms of iterations, on my machine this takes less than 20 seconds to do the 5000 iterations, and it has clearly peaked out by then (both in sample 2011 and out of sample 2012).
I’ve loading the RTM model object with a few helper functions, so if you then run print( model.coef_table() ), you get out the final regression coefficients, including the dispersion term. For my negative binomial models for my dissertation, the dispersion term tended to be around ~4 for many models, so this corresponds pretty closely with my prior work.
These have interpretations as latent variables representing the effect of nearby alcohol outlets (both distance and density), metro entrances (just distance), and 311 calls for service (just density). Similar to original RTM, I have restricted the crime generator effects to be positive.
I also have another helper function, model.loadings(), that gives you a nice table. Here this shows how the original variables contribute to the latent variable. So here are the loadings for the distance to the nearest metro.
You can see that the dummy variables for met_dis_300 (meters) and smaller all contribute to the latent variable. So instead of picking one variable in the end, it allows multiple variables to contribute to the latent risk score. It may make more sense in this set up to encode variables as not cumulative, e.g. < 50 meters, < 100 meters, but orthogonal, e.g. [0,50),[50,100), etc.), but just stuck with the prior data in the same format for now. I force the loadings to sum to 1 and be positive, so the latent variables still have a very apples-to-apples comparison in terms of effect sizes.
Here are the loadings for alcohol outlets, so we have both some distance and density effects in the end.
And here are the loadings for 311 density variables:
So you can see for the last one, only the furthest away had an effect at all. Which is contra to the broken windows theory! But also shows that this is more general than the original RTM approach. If it only should be one variable the model will learn that, but if it should be more it will incorporate a wider array of weights.
Next is to check out how well the model does overall. For calibration for Poisson/Negative Binomial models, I just detach my pytorch tensors, and feed them into my functions to do the evaluations.
#Calibration for Negative Binomial predictions
pred_pd = pd.Series( y_pred.exp().detach().numpy() )
disp_val = model.dispersion.exp().item()
nb_fit = dl_rtm_funcs.nb_fit(mu=pred_pd, obs=crime_data['Viol_2011'],
disp=disp_val, max_y=10)
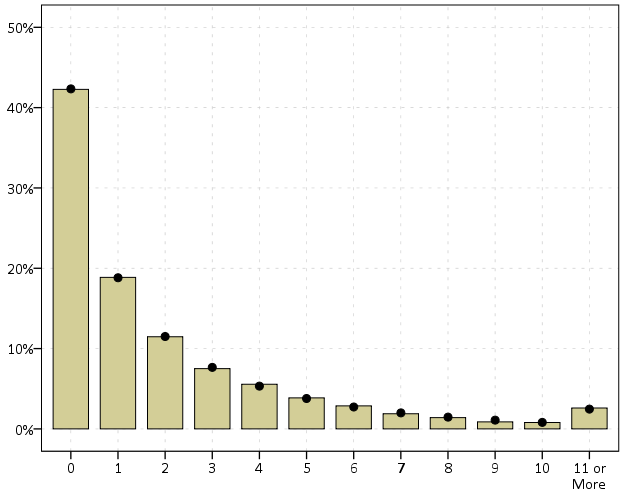
print( nb_fit )So this shows that the model is pretty well calibrated in terms of overall predictions. Both samples predict 83% zeroes. I predict a few more 3/4 crime areas than observed, and my tails are somewhat thinner than they should be, but only by a tiny bit. (No doubt this would improve if I incorporated more covariates, kept it simple to debug on purpose.)
We can ignore the negative binomial dispersion term and see what our model would predict in the usual Poisson case (the mean functions are the same, it is just changing the variance). To do this, just pass in a dispersion term of 1.
pois_fit = dl_rtm_funcs.nb_fit(mu=pred_pd, obs=crime_data['Viol_2011'],
disp=1, max_y=10)
print( pois_fit )You can see that the Poisson model is a much worse fit. Underpredicting zero crime areas by 6%, and areas with over 10 crimes should pretty much never happen according to the Poisson model.
We should be assessing these metrics out of sample as well, and you can see that given crime is very historically stable, the out of sample 2012 violent crime counts are similarly well calibrated.
Finally, I have suggested in the past to use a weighted ROC curve as a metric for crime counts. Here is a simple example of doing that in python.
crime_data['Weights'] = crime_data['Viol_2012'].clip(1)
crime_data['Outcome'] = crime_data['Viol_2012'].clip(0,1)
fpr, tpr, thresh = roc_curve(crime_data['Outcome'], pred_pd, sample_weight=crime_data['Weights'])
weighted_auc = auc(fpr, tpr)
print( weighted_auc ) So you can see the AUC is nothing to brag about here, 0.61 (it is only 0.63 in the 2011 sample). But again I am sure I could get that up by quite a bit by incorporating more covariates into the model.