For one of my classes for PhD students (in seminar research and analysis), I talk about the distinction between random effect models and fixed effect models for a week.
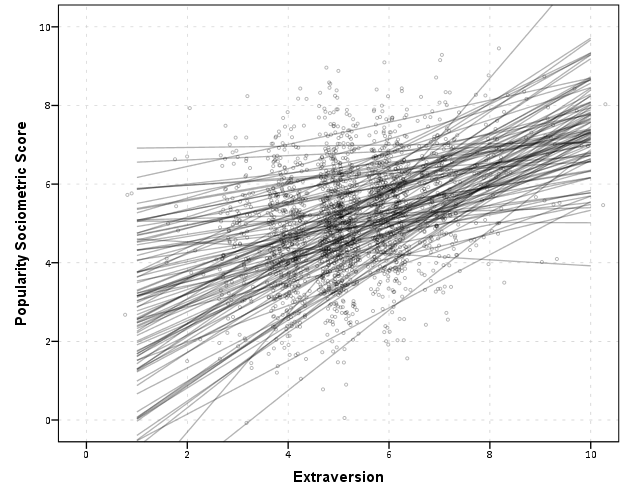
One of my favorite plots to go with random effect models is called a caterpillar plot. So typically folks just stop at reporting the variance of the random intercepts and slopes when they estimate these models. But you not only get the global variance estimates, but can also get an estimate (and standard error) for each higher level variable. So if I have 100 people, and I do a random intercept for those 100 people, I can say “Joe B’s random intercept is 0.5, and Jane Doe’s random intercept is -0.2” etc.
So this is halfway in between confirmatory data analysis (we used a model to get those estimates) but is often useful for further understanding the model and seeing if you should add anything else. E.g. if you see the random intercepts have a high correlation with some other piece of person information, that information should be incorporated into the model. It is also useful to spot outliers. And if you have spatial data mapping the random intercepts should be something you do.
SPSS recently made it easier to make these types of plot (as of V25), so I am going to give an example. In my class, I give code examples in R, Stata, and SPSS whenever I can, so this link contains code for all three programs. I will be using data from my dissertation, with crime on street segments in DC, nested within regular grid cells (used to approximate neighborhoods).
SPSS Code
So first data prep, I define where my data is using FILE HANDLE, read in the csv file of the data, compute a new variable (the sum of both detritus and physical infrastructure 311 calls). Then finally I declare that the FishID variable (my grid cells neighborhoods) is a nominal level variable. SPSS needs that defined correctly for later models.
*************************************************************.
FILE HANDLE data /NAME = "??????Your Path Here!!!!!!!!!!!".
*Importing the CSV file into SPSS.
GET DATA /TYPE=TXT
/FILE="data\DC_Crime_withAreas.csv"
/ENCODING='UTF8'
/DELCASE=LINE
/DELIMITERS=","
/QUALIFIER='"'
/ARRANGEMENT=DELIMITED
/FIRSTCASE=2
/DATATYPEMIN PERCENTAGE=95.0
/VARIABLES=
MarID AUTO
XMeters AUTO
YMeters AUTO
FishID AUTO
XMetFish AUTO
YMetFish AUTO
TotalArea AUTO
WaterArea AUTO
AreaMinWat AUTO
TotalLic AUTO
TotalCrime AUTO
CFS1 AUTO
CFS2 AUTO
CFS1Neigh AUTO
CFS2Neigh AUTO
/MAP.
CACHE.
EXECUTE.
DATASET NAME CrimeDC.
DATASET ACTIVATE CrimeDC.
*Compute a new variable, total number of 311 calls for service.
COMPUTE CFS = CFS1 + CFS2.
EXECUTE.
VARIABLE LEVEL FishID (NOMINAL).
*************************************************************.Now onto the good stuff, estimating our model. Here we are looking at the fixed effects of bars and 311 calls on crime on street segments, but also estimating a random intercept for each grid cell. As of V25, SPSS lets you specify an option to print the solution for the random statements, which we can capture in a new SPSS dataset using the OMS command.
So first we declare our new dataset to dump the results in, Catter. Then we specify an OMS command to capture the random effect estimates, and then estimate our negative binomial model. I swear SPSS did not use to be like this, but now you need to end the OMS command before you putz with that dataset.
*************************************************************.
DATASET DECLARE Catter.
OMS
/SELECT TABLES
/IF SUBTYPES='Empirical Best Linear Unbiased Predictions'
/DESTINATION FORMAT=SAV OUTFILE='Catter' VIEWER=YES
/TAG='RandTable'.
*SOLUTION option only as of V25.
GENLINMIXED
/FIELDS TARGET=TotalCrime
/TARGET_OPTIONS DISTRIBUTION=NEGATIVE_BINOMIAL
/FIXED EFFECTS=TotalLic CFS
/RANDOM USE_INTERCEPT=TRUE SUBJECTS=FishID SOLUTION=TRUE
/SAVE PREDICTED_VALUES(PredRanEff).
OMSEND TAG='RandTable'.
EXECUTE.
DATASET ACTIVATE Catter.
*************************************************************.And now we can navigate over to the saved table and make our caterpillar plot. Because we have over 500 areas, I sort the results and don’t display the X axis. But this lets you see the overall distribution and spot any outliers.
*************************************************************.
*Lets make a caterpillar plot.
FORMATS Prediction Std.Error LowerBound UpperBound (F4.2).
SORT CASES BY Prediction (D).
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=Var1 Prediction LowerBound UpperBound
/GRAPHSPEC SOURCE=INLINE
/FRAME INNER=YES.
BEGIN GPL
SOURCE: s=userSource(id("graphdataset"))
DATA: Var1=col(source(s), name("Var1"), unit.category())
DATA: Prediction=col(source(s), name("Prediction"))
DATA: LowerBound=col(source(s), name("LowerBound"))
DATA: UpperBound=col(source(s), name("UpperBound"))
SCALE: cat(dim(1), sort.data())
GUIDE: axis(dim(1), null())
GUIDE: axis(dim(2), label("BLUP"))
SCALE: linear(dim(2), include(0))
ELEMENT: edge(position(region.spread.range(Var1*(LowerBound + UpperBound))), size(size."0.5")))
ELEMENT: point(position(Var1*Prediction), color.interior(color.black), size(size."1"))
END GPL.
*************************************************************.And here is my resulting plot.
And I show in the linked code some examples for not only random intercepts, but you can do the same thing for random slopes. Here is an example doing a model where I let the TotalLic effect (the number of alcohol licenses on the street segment) vary by neighborhood grid cell. (The flat 0 estimates and consistent standard errors are grid cells with 0 licenses in the entire area.)
The way to interpret these estimates are as follows. The fixed effect part of the regression equation here is: 0.247 + 0.766*Licenses. That alcohol license effect though varies across the study area, some places have a random slope of +2, so the equation could then be thought of as 0.247 + (0.766 + 2)*Licenses (ignoring the random intercept part). So the effect of bars in that area is much larger. Also there are places with negative effects, so the effects of bars in those places are smaller. You can do the same type of thought experiments simply with the reported variance components, but I find the caterpillar plots to be a really good visual to show what those random effects actually mean.
For other really good multilevel modelling resources, check out the Centre for Multilevel Modelling, and Germán Rodríguez’s online notes. Eventually I will get around to uploading my seminar class notes and code snippets, but in the mean time if you see a week and would like my code examples, always feel free to email.