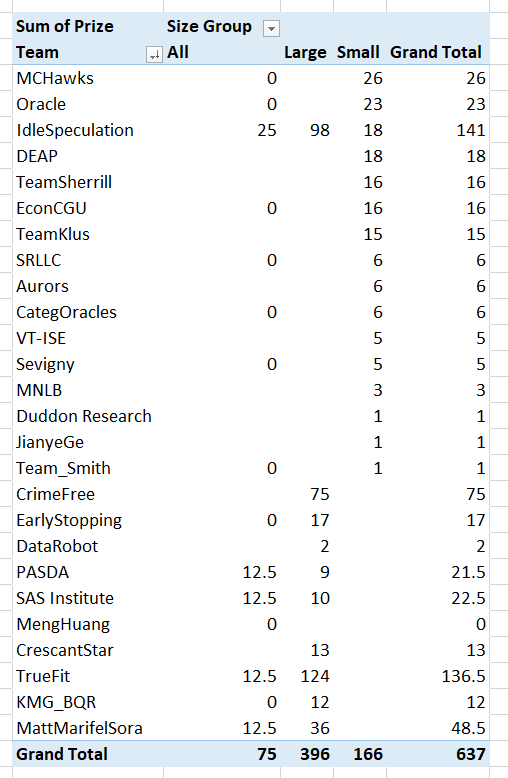
In doing a post mortem on our results for the NIJ recidivism challenge, first I calculated the extent to which our predictions would have done better if we did not bias our predictions to meet the fairness challenge. In the end, for Round 1 our team would have been in 3rd or 4th place for the small team rankings if we went with the unbiased predictions. It ended up being it only increased our Brier score by around ~0.001-0.002 though for each. (So I am glad we biased with a chance to win the fairness competition in the end.)
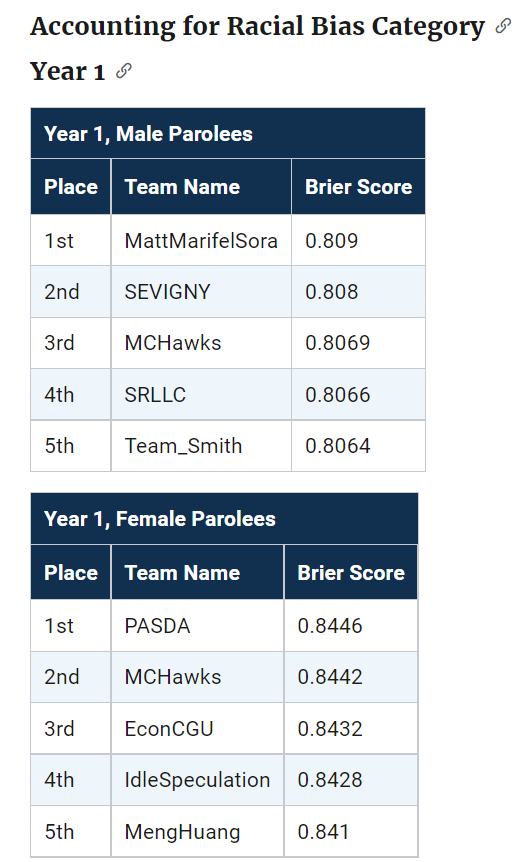
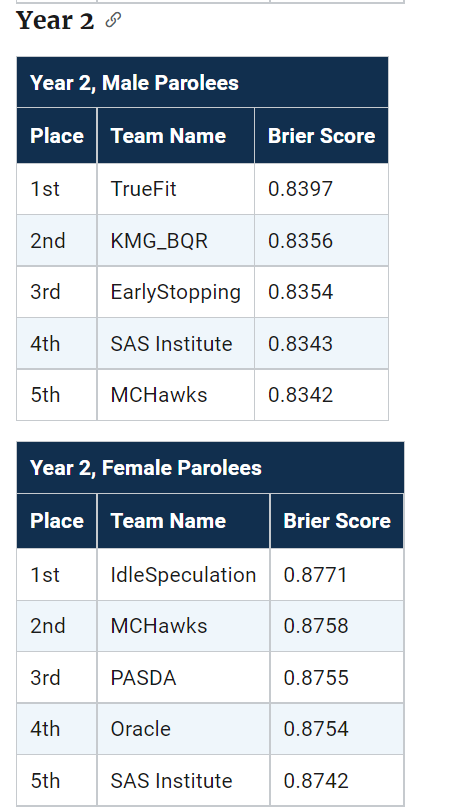
The leaderboards are so tight across the competition, often you need to go to the fourth decimal to determine the rankings. Here are the rankings for Round 1 Brier Scores for the small team:

Ultimately these metrics used to determine the rankings are themselves statistics measured with error. So here I did a simulation to see the extent that these metrics had error.
These are not exactly the models we ended up using, but are very close (only performed slightly worse than the ones we ended up going with), but here I will show an example in python comparing rankings between a logit regression with L1 penalties vs a lightboosted model. So for some upfront on the python libraries I will be using, and I download the data directly:
import numpy as np
import pandas as pd
from scipy.stats import binom
from sklearn.linear_model import LogisticRegression
from lightgbm import LGBMClassifier
from sklearn.metrics import roc_auc_score, brier_score_loss
full_data = pd.read_csv('https://data.ojp.usdoj.gov/api/views/ynf5-u8nk/rows.csv?accessType=DOWNLOAD',index_col='ID')
The next part is just encoding the data. I am doing this for R1, so only using a certain set of information.
# Numeric Impute
num_imp = ['Gang_Affiliated','Supervision_Risk_Score_First',
'Prior_Arrest_Episodes_DVCharges','Prior_Arrest_Episodes_GunCharges',
'Prior_Conviction_Episodes_Viol','Prior_Conviction_Episodes_PPViolationCharges',
'Residence_PUMA']
# Ordinal Encode (just keep puma as is)
ord_enc = {}
ord_enc['Gender'] = {'M':1, 'F':0}
ord_enc['Race'] = {'WHITE':0, 'BLACK':1}
ord_enc['Age_at_Release'] = {'18-22':6,'23-27':5,'28-32':4,
'33-37':3,'38-42':2,'43-47':1,
'48 or older':0}
ord_enc['Supervision_Level_First'] = {'Standard':0,'High':1,
'Specialized':2,'NA':-1}
ord_enc['Education_Level'] = {'Less than HS diploma':0,
'High School Diploma':1,
'At least some college':2,
'NA':-1}
ord_enc['Prison_Offense'] = {'NA':-1,'Drug':0,'Other':1,
'Property':2,'Violent/Non-Sex':3,
'Violent/Sex':4}
ord_enc['Prison_Years'] = {'Less than 1 year':0,'1-2 years':1,
'Greater than 2 to 3 years':2,'More than 3 years':3}
# _more clip
more_clip = ['Dependents','Prior_Arrest_Episodes_Felony','Prior_Arrest_Episodes_Misd',
'Prior_Arrest_Episodes_Violent','Prior_Arrest_Episodes_Property',
'Prior_Arrest_Episodes_Drug',
'Prior_Arrest_Episodes_PPViolationCharges',
'Prior_Conviction_Episodes_Felony','Prior_Conviction_Episodes_Misd',
'Prior_Conviction_Episodes_Prop','Prior_Conviction_Episodes_Drug']
# Function to prep data as I want, label encode
# And missing imputation
def prep_data(data,ext_vars=['Recidivism_Arrest_Year1','Training_Sample']):
cop_dat = data.copy()
# Numeric impute
for n in num_imp:
cop_dat[n] = data[n].fillna(-1).astype(int)
# Ordinal Recodes
for o in ord_enc.keys():
cop_dat[o] = data[o].fillna('NA').replace(ord_enc[o]).astype(int)
# _more clip
for m in more_clip:
cop_dat[m] = data[m].str.split(' ',n=1,expand=True)[0].astype(int)
# Only keeping variables of interest
kv = ext_vars + num_imp + list(ord_enc.keys()) + more_clip
return cop_dat[kv].astype(int)
pdata = prep_data(full_data)
I did smart ordinal encoding, minus the missing data. So logit models are not super crazy with this data, although dummy variables + imputatation are likely a better approach (I am just being lazy here). But those should not be an issue for the tree based boosted models. Here I estimate models using the original train/test split chosen by NIJ:
y_var = 'Recidivism_Arrest_Year1'
x_vars = list(pdata)
x_vars.remove(y_var)
x_vars.remove('Training_Sample')
cat_vars = list( set(x_vars) - set(more_clip) )
l1 = LogisticRegression(penalty='l1', solver='liblinear')
lb = LGBMClassifier(silent=True)
# Original train/test split
train = pdata[pdata['Training_Sample'] == 1].copy()
test = pdata[pdata['Training_Sample'] == 0].copy()
# Fit models, and then eval on out of sample
l1.fit(train[x_vars],train[y_var])
lb.fit(train[x_vars],train[y_var],feature_name=x_vars,categorical_feature=cat_vars)
l1pp = l1.predict_proba(test[x_vars])[:,1]
lbpp = lb.predict_proba(test[x_vars])[:,1]
And then we can see how our two models do in this scenario according to the AUC or the Brier score statistic.
# ROC for the models
aucl1 = roc_auc_score(test[y_var],l1pp)
auclb = roc_auc_score(test[y_var],lbpp)
print(f'AUC L1 {aucl1}, AUC LightBoosted {auclb}')
# Brier score for models
bsl1 = brier_score_loss(test[y_var],l1pp)
bslb = brier_score_loss(test[y_var],lbpp)
print(f'Brier L1 {bsl1}, Brier LightBoosted {bslb}')

So you can see that the L1 model wins over the light boosted model (despite the wonky encoding with missing data) for both the AUC (+0.002) and the Brier Score (+0.001). (Note this is for the pooled sampled for both males/females.)
But is this just luck of the draw for the particular train/test dataset? That is, when we chose another train/test split, but fit the same models, would the light boosted model win some of the time? Here I do that, using the approximately 70% train/test split, but make it random and then estimate the test set Brier/AUC.
res = [] #list to stuff results into
for i in range(1000):
print(f'Round {i}')
rand_train = binom.rvs(1,0.7,size=pdata.shape[0])
train = pdata[rand_train == 1].copy()
test = pdata[rand_train == 0].copy()
l1.fit(train[x_vars],train[y_var])
lb.fit(train[x_vars],train[y_var],feature_name=x_vars,categorical_feature=cat_vars)
l1pp = l1.predict_proba(test[x_vars])[:,1]
lbpp = lb.predict_proba(test[x_vars])[:,1]
aucl1 = roc_auc_score(test[y_var],l1pp)
auclb = roc_auc_score(test[y_var],lbpp)
bsl1 = brier_score_loss(test[y_var],l1pp)
bslb = brier_score_loss(test[y_var],lbpp)
loc_tup = (i,aucl1,auclb,bsl1,bslb)
res.append(loc_tup)
fin_data = pd.DataFrame(res,columns=['Iter','AUCL1','AUCLB','BSL1','BSLB'])
fin_data.describe().T
# L1 wins for Brier score
(fin_data['BSL1'] < fin_data['BSLB']).mean()
# L1 wins for AUC
(fin_data['AUCL1'] > fin_data['AUCLB']).mean()

So you can see that the standard deviation for AUC is around 0.005, and the Brier Score is 0.002, also based on the means/min/max we can see that these two models have quite a bit of overlap in the distribution.
But, the results are correlated – when L1 tends to do worse, lightboosted also does worse. So when we look at the rankings, in this scenario L1 wins the majority of the time (but not always). This suggests to me that it was a good thing NIJ did not use AUC to judge, Brier scores seem much less volatile than AUC in this sample.
We can check out the correlations between the scores. AUC only has a correlation of around 0.8, whereas Brier has a correlation of 0.9. (If correlations were 1 the train/test split wouldn’t matter, the same person would always win in the rankings.)
# Results tend to be fairly correlated
fin_data.corr()
fin_data.cov()

But despite these models having a clear winner in this example, the margins between these two models are larger than the margins in the typical leaderboards. So I did a simulation using the observed leaderboard Brier scores for males for R1 as the means, and used the variance/covariance estimates above to make random draws.
This shows us, given the four observed leaderboard metrics, and my guesstimates for the typical error, how often will the leaders flip. Tighter scores and larger variances mean more flips.
# Simulation to see how often rankings flip
mu = np.array([0.1916, 0.1919, 0.1920, 0.1922])
tv = len(mu)
sd = 0.002 # sd and corr based on my earlier simulation
cor = 0.9
var = sd**2
cov = cor*(sd**2)
# filling the var/covariance matrix
r = np.ones((tv,tv)) * cov
np.fill_diagonal(r, var)
# Generating random multivariate normal
np.random.seed(10)
y = np.random.multivariate_normal(mu, r, size=1000)
y_ranks = y.argsort(axis=1)
# Making a nicer long dataset to see how often ranks swapped
persons = ['IdleSpeculation','SRLLC','Sevigny','TeamSmith']
y_rankdf = pd.DataFrame(y_ranks,columns=persons)
longy = y_rankdf.melt()
# How often are the ranks switched?
pd.crosstab(longy['variable'],longy['value'], normalize='columns')

How to read this table is that in the observed data for small team Males Round 1, IdleSpeculation was Ranked #1 with a Brier Score of 0.1916. My simulations show that based on those prior estimates, IdleSpeculation takes the top prize the most often (column 0), but only 43% of the time. You can see that even the bottom score here by TeamSmith takes #1 in 10% of the simulations.
This shows that there is some signal in the leaderboard, if it was totally random each of the ranks would have ~25% in each outcome. But it is clearly far from certain though either. This only considers people on the leaderboard who I know their results. It could also easily be someone in 5,6,7 could even have swapped to the #1 results.
What can we learn from this? One, the leaderboard results are unlikely to signify substantively improved models between different competitors. Clearly IdleSpeculation did well across the entire competition, but it would be hard to argue they were clearly better than everyone else (e.g. IdleSpeculations #3 rank in females in round 1 I suspect is just as likely due to bad luck as it is to their model being substantively worse than TeamKlus or TeamSherill).
Two, I think it would be better for competitions like this for people to submit algorithms, and then the algorithms can be judged on various train/tests (or a grid search cross-validation, or whatever). Using a simple train/test split like this will always come with some noise in the rankings.
This also solves the issue with transparency. Currently NIJ is simply asking us to submit a paper saying how we did the results. It would be more transparent to force people to submit code to replicate the results 100% (as well as prevent any obvious cheating).