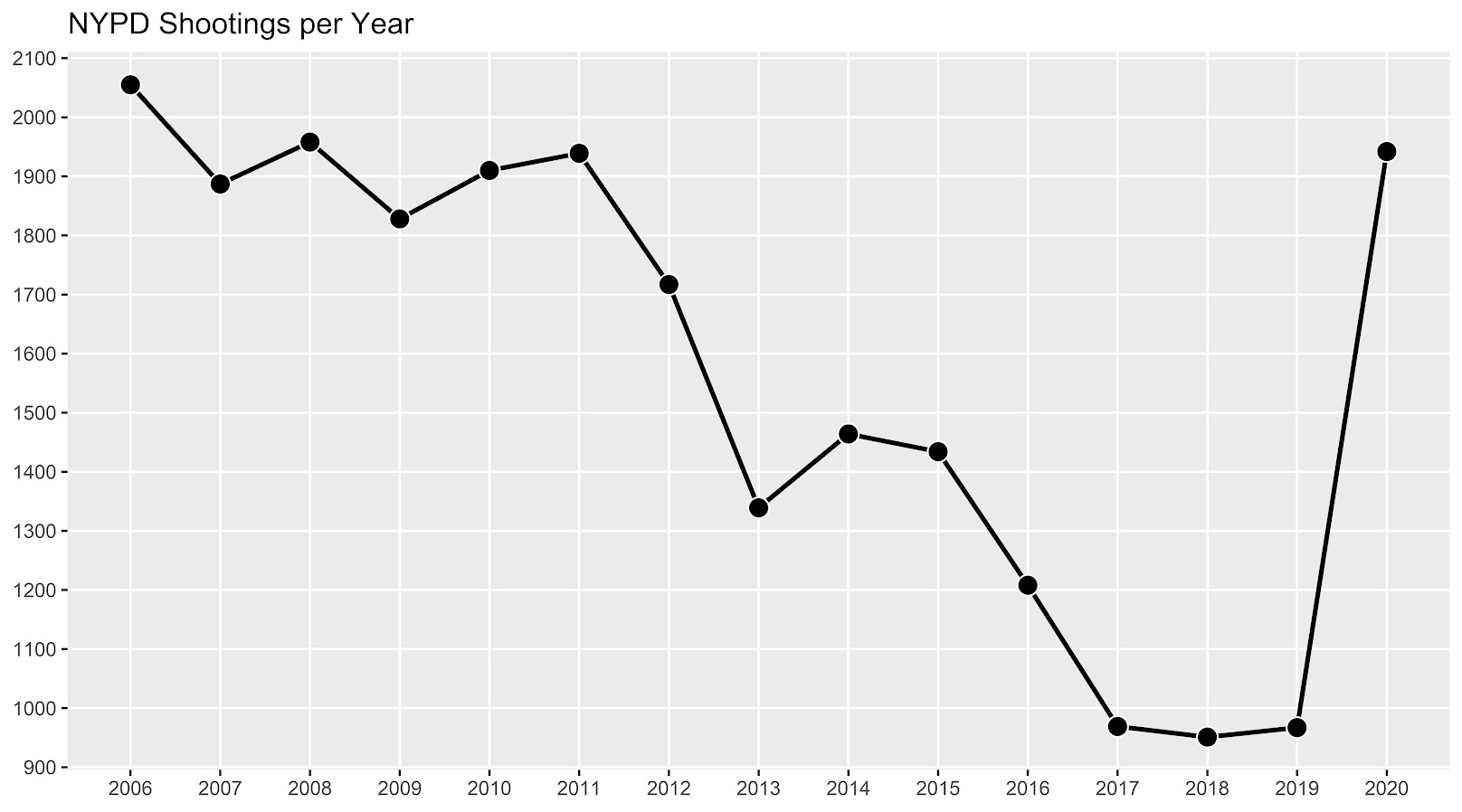
If you had asked me at the start of widespread Covid lockdown measures what the effect would be on crime, I am pretty sure I would have guessed it will make crime go down. Fewer people out and about causes fewer interactions that can lead to a crime. That isn’t how it has shaped up though, quite a few places have seen increases in serious violent crime. One of the most dramatic examples of this is that shootings in NYC doubled from 900 in 2019 to over 1800 in 2020. I am going to show how to generate this chart later via some R code, but it is easier to show than to say. NYPD’s open data on shootings (historical, current) go back to 2006.
I know I am critical on this site of folks overinterpreting crime increases, for example going from 20 to 35 is pretty weak evidence of an increase given the inherent variance for low count Poisson data (a Poisson e-test has a p-value of 0.04 in that case). But going from 900 to 1800 is a much clearer signal.
Jerry Ratcliffe recently posted an R library to do his crime dispersion analysis, so I figured this would be an excellent example use case. The idea behind this analysis is spatial – we know there is a crime increase, but did the increase happen everywhere, or did it just happen in a few locations. Here I am going to use the NYPD shooting data aggregated at the precinct level to test this.
As another note, while I often use micro-spatial units of analysis in my work, this method, along with others (such as the sppt test), are just not going to work out for very low count, very tiny spatial units of analysis. I would suggest offhand to only do this analysis if the spatial units of analysis under study have an average of at least 10 crimes per area in the pre time period. Which is right about on the mark for the precinct analysis in NYC.
Here is the data and R code to follow along, below I will give a walkthrough.
Crime increase dispersion analysis in R
So first as some front matter, I load in my libraries (Jerry’s crimedispersion you can install from github via devtools, see his page for an example), and the function I define here I’ve gone over in a prior blog post of mine as well.
###############################
library(ggplot2)
library(crimedispersion)
# Increase contours, see https://andrewpwheeler.com/2020/02/21/some-additional-plots-to-go-with-crime-increase-dispersion/
make_cont <- function(pre_crime,post_crime,levels=c(-3,0,3),lr=10,hr=max(pre_crime)*1.05,steps=1000){
#calculating the overall crime increase
ov_inc <- sum(post_crime)/sum(pre_crime)
#Making the sequence on the square root scale
gr <- seq(sqrt(lr),sqrt(hr),length.out=steps)^2
cont_data <- expand.grid(gr,levels)
names(cont_data) <- c('x','levels')
cont_data$inc <- cont_data$x*ov_inc
cont_data$lines <- cont_data$inc + cont_data$levels*sqrt(cont_data$inc)
return(as.data.frame(cont_data))
}
my_dir <- 'D:\\Dropbox\\Dropbox\\Documents\\BLOG\\NYPD_ShootingIncrease\\Analysis'
setwd(my_dir)
###############################
Now we are ready to import our data and stack them into a new data frame. (These are individual incident level shootings, not aggregated. If I ever get around to it I will do an analysis of fatality and distance to emergency rooms like I did with the Philly data.)
###############################
# Get the NYPD data and stack it
# From https://data.cityofnewyork.us/Public-Safety/NYPD-Shooting-Incident-Data-Year-To-Date-/5ucz-vwe8
# And https://data.cityofnewyork.us/Public-Safety/NYPD-Shooting-Incident-Data-Historic-/833y-fsy8
# On 2/1/2021
old <- read.csv('NYPD_Shooting_Incident_Data__Historic_.csv', stringsAsFactors=FALSE)
new <- read.csv('NYPD_Shooting_Incident_Data__Year_To_Date_.csv', stringsAsFactors=FALSE)
# Just one column off
print( cbind(names(old), names(new)) )
names(new) <- names(old)
shooting <- rbind(old,new)
###############################
Now we just want to do aggregate counts of these shootings per year and per precinct. So first I substring out the year, then use table to get aggregate counts in R, then make my nice time series graph using ggplot.
###############################
# Create the current year and aggregate
shooting$Year <- substr(shooting$OCCUR_DATE, 7, 10)
year_stats <- as.data.frame(table(shooting$Year))
year_stats$Year <- as.numeric(as.character(year_stats$Var1))
year_plot <- ggplot(data=year_stats, aes(x=Year,y=Freq)) +
geom_line(size=1) + geom_point(shape=21, colour='white', fill='black', size=4) +
scale_y_continuous(breaks=seq(900,2100,by=100)) +
scale_x_continuous(breaks=2006:2020) +
theme(axis.title.x=element_blank(), axis.title.y=element_blank(),
panel.grid.minor = element_blank()) +
ggtitle("NYPD Shootings per Year")
year_plot
# Not quite the same as Petes, https://copinthehood.com/shooting-in-nyc-2020/
###############################

Part of the reason I do this is not because I don’t trust Pete’s analysis, but because I don’t want to embed pictures from someone elses website! So wanted to recreate the time series graph myself. So next up we need to do the same aggregating, but not for the whole city, but by each precinct. You can use the same table method again, but simply pass in additional columns. That gets you the data in long format, so then I reshape it to wide for later analysis (so each row is a single precinct and each column is a yearly count of shootings). (Note there have been some splits in precincts over the years IIRC, I don’t worry about that here, will cause it to be 0,0 in the 2019/2020 data I look at.)
###############################
#Now aggregating to year and precinct
counts <- as.data.frame(table(shooting$Year, shooting$PRECINCT))
names(counts) <- c('Year','PCT','Count')
# Reshape long to wide
count_wide <- reshape(counts, idvar = "PCT", timevar = "Year", direction = "wide")
###############################
And now we can give Jerry’s package a test run, where you just pass it your variable names.
# Jerrys function for crime increase dispersion
output <- crimedispersion(count_wide, 'PCT', 'Count.2019', 'Count.2020')
output

The way to understand this is in a hypothetical world in which we could reduce shootings in one precinct at a time, we would need to reduce shootings in 57 of the 77 precincts to reduce 2020 shootings to 2019 levels. So this suggests very widespread increases, it isn’t just concentrated among a few precincts.
Another graph I have suggested to explore this, while taking into account the typical variance with Poisson count data, is to plot the pre crime counts on the X axis, and the post crime counts on the Y axis.
###############################
# My example contour with labels
cont_lev <- make_cont(count_wide$Count.2019, count_wide$Count.2020, lr=5)
eq_plot <- ggplot() +
geom_line(data=cont_lev, color="darkgrey", linetype=2,
aes(x=x,y=lines,group=levels)) +
geom_point(data=count_wide, shape = 21, colour = "black", fill = "grey", size=2.5,
alpha=0.8, aes(x=Count.2019,y=Count.2020)) +
scale_y_continuous(breaks=seq(0,140,by=10) +
scale_x_continuous(breaks=seq(0,70,by=5)) +
coord_cartesian(ylim = c(0, 140)) +
xlab("2019 Shootings Per Precinct") + ylab("2020 Shootings")
eq_plot
###############################

The contour lines show the hypothesis that crime increased (by around 100% here). So if a point is near the middle line, it follows that doubled mark almost exactly. The upper/lower lines indicate the typical variance, which is a very good fit to the data here you can see. Very few points are outside the boundaries.
Both of these analyses point to the fact that shooting increases were widespread across NYC precincts. Pretty much everywhere doubled in the number of shootings, it is just some places had a larger baseline to double than others (and the data has some noise, you can pick out some places that did not increase if you cherry pick the data).
And as a final R note, if you want to save these graphs as a nice high resolution PNG, here is an example with Jerry’s dispersion object:
# Saving dispersion plot as a high res PNG
png(file = "ODI.png", bg = "transparent", height=5, width=9, units="in", res=1000, type="cairo")
output #this is the object from Jerrys crimedispersion() function earlier
dev.off()
Going forward I am wondering if there is a good way to do spatial monitoring for crime data like this, like some sort of control chart that takes into account both space and time. So isn’t retrospective a year later recap, but in near real time identify spatial increases.
Other References of Interest
- Justin Nix & company have a few blog posts looking at NYC data as well. In the first they talk about the variance in cities, many are up but several are down as well in violence. A later post though updated with the clear increase in shootings in NYC.
- There are too many papers at this point for me to do a bibliography of all the Covid and crime updates, but two open examples are Matt Ashby did a paper on several US cities, and Campedelli et al have an analysis of Chicago. Each show variance again, so no universal up or down in trends, but various examples of increases or decreases both between cities and between different crime types within a city.

