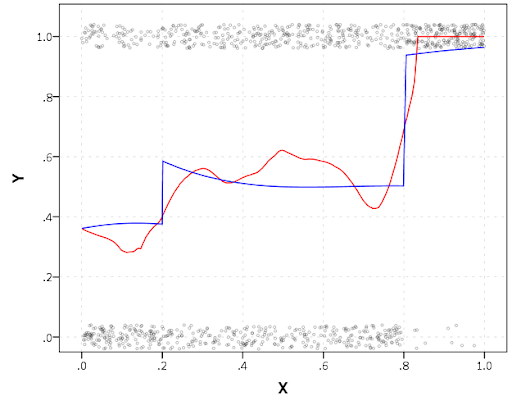
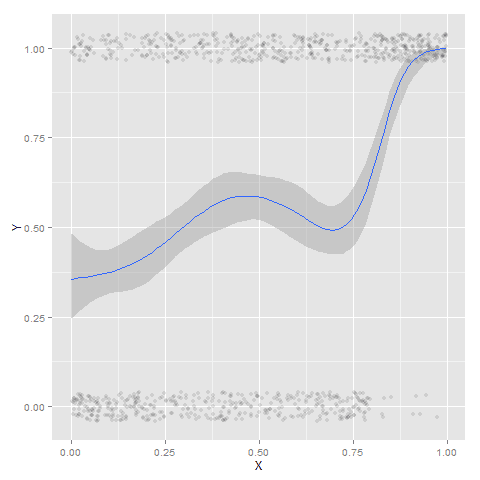
The other day I made a blog post on my notes on making scatterplots in matplotlib. One big chunk of why you want to make scatterplots though is if you are interested in a predictive relationship. Typically you want to look at the conditional value of the Y variable based on the X variable. Here are some example exploratory data analysis plots to accomplish that task in python.
I have posted the code to follow along on github here, in particular smooth.py has the functions of interest, and below I have various examples (that are saved in the Examples_Conditional.py file).
Data Prep
First to get started, I am importing my libraries and loading up some of the data from my dissertation on crime in DC at street units. My functions are in the smooth set of code. Also I change the default matplotlib theme using smooth.change_theme(). Only difference from my prior posts is I don’t have gridlines by default here (they can be a bit busy).
#################################
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import os
import sys
mydir = r'D:\Dropbox\Dropbox\PublicCode_Git\Blog_Code\Python\Smooth'
data_loc = r'https://dl.dropbox.com/s/79ma3ldoup1bkw6/DC_CrimeData.csv?dl=0'
os.chdir(mydir)
#My functions
sys.path.append(mydir)
import smooth
smooth.change_theme()
#Dissertation dataset, can read from dropbox
DC_crime = pd.read_csv(data_loc)
#################################Binned Conditional Plots
The first set of examples, I bin the data and estimate the conditional means and standard deviations. So here in this example I estimate E[Y | X = 0], E[Y | X = 1], etc, where Y is the total number of part 1 crimes and x is the total number of alcohol licenses on the street unit (e.g. bars, liquor stores, or conv. stores that sell beer).
The function name is mean_spike, and you pass in at a minimum the dataframe, x variable, and y variable. I by default plot the spikes as +/- 2 standard deviations, but you can set it via the mult argument.
####################
#Example binning and making mean/std dev spike plots
smooth.mean_spike(DC_crime,'TotalLic','TotalCrime')
mean_lic = smooth.mean_spike(DC_crime,'TotalLic','TotalCrime',
plot=False,ret_data=True)
####################This example works out because licenses are just whole numbers, so it can be binned. You can pass in any X variable that can be binned in the end. So you could pass in a string for the X variable. If you don’t like the resulting format of the plot though, you can just pass plot=False,ret_data=True for arguments, and you get the aggregated data that I use to build the plots in the end.
mean_lic = smooth.mean_spike(DC_crime,'TotalLic','TotalCrime',
plot=False,ret_data=True)Another example I am frequently interested in is proportions and confidence intervals. Here it uses exact binomial confidence intervals at the 99% confidence level. Here I clip the burglary data to 0/1 values and then estimate proportions.
####################
#Example with proportion confidence interval spike plots
DC_crime['BurgClip'] = DC_crime['OffN3'].clip(0,1)
smooth.prop_spike(DC_crime,'TotalLic','BurgClip')
####################A few things to note about this is I clip out bins with only 1 observation in them for both of these plots. I also do not have an argument to save the plot. This is because I typically only use these for exploratory data analysis, it is pretty rare I use these plots in a final presentation or paper.
I will need to update these in the future to jitter the data slightly to be able to superimpose the original data observations. The next plots are a bit easier to show that though.
Restricted Cubic Spline Plots
Binning like I did prior works out well when you have only a few bins of data. If you have continuous inputs though it is tougher. In that case, typically what I want to do is estimate a functional relationship in a regression equation, e.g. Y ~ f(x), where f(x) is pretty flexible to identify potential non-linear relationships.
Many analysts are taught the loess linear smoother for this. But I do not like loess very much, it is often both locally too wiggly and globally too smooth in my experience, and the weighting function has no really good default.
Another popular choice is to use generalized additive model smoothers. My experience with these (in R) is better than loess, but they IMO tend to be too aggressive, and identify overly complicated functions by default.
My favorite approach to this is actually then from Frank Harrell’s regression modeling strategies. Just pick a regular set of restricted cubic splines along your data. It is arbitrary where to set the knot locations for the splines, but my experience is they are very robust (so chaning the knot locations only tends to change the estimated function form by a tiny bit).
I have class notes on restricted cubic splines I think are a nice introduction. First, I am going to make the same dataset from my class notes, the US violent crime rate from 85 through 2010.
years = pd.Series(list(range(26)))
vcr = [1881.3,
1995.2,
2036.1,
2217.6,
2299.9,
2383.6,
2318.2,
2163.7,
2089.8,
1860.9,
1557.8,
1344.2,
1268.4,
1167.4,
1062.6,
945.2,
927.5,
789.6,
734.1,
687.4,
673.1,
637.9,
613.8,
580.3,
551.8,
593.1]
yr_df = pd.DataFrame(zip(years,years+1985,vcr), columns=['y1','years','vcr'])I have a function that allows you to append the spline basis to a dataframe. If you don’t pass in a data argument, in returns a dataframe of the basis functions.
#Can append rcs basis to dataframe
kn = [3.0,7.0,12.0,21.0]
smooth.rcs(years,knots=kn,stub='S',data=yr_df)I also have in the code set Harrell’s suggested knot locations for the data. This ranges from 3 to 7 knots (it will through an error if you pass a number not in that range). This here suggests the locations [1.25, 8.75, 16.25, 23.75].
#If you want to use Harrell's rules to suggest knot locations
smooth.sug_knots(years,4)Note if you have integer data here these rules don’t work out so well (can have redundant suggested knot locations). So Harell’s defaults don’t work with my alcohol license data. But it is one of the reasons I like these though, I just pick regular locations along the X data and they tend to work well. So here is a regression plot passing in those knot locations kn = [3.0,7.0,12.0,21.0] I defined a few paragraphs ago, and the plot does a few vertical guides to show the knot locations.
#RCS plot
smooth.plot_rcs(yr_df,'y1','vcr',knots=kn)Note that the error bands in the plot are confidence intervals around the mean, not prediction intervals. One of the nice things though about this under the hood, I used statsmodels glm interface, so if you want you can change the underlying link function to Poisson (I am going back to my DC crime data here), you just pass it in the fam argument:
#Can pass in a family argument for logit/Poisson models
smooth.plot_rcs(DC_crime,'TotalLic','TotalCrime', knots=[3,7,10,15],
fam=sm.families.Poisson(), marker_size=12)This is a really great example for the utility of splines. I will show later, but a linear Poisson model for the alcohol license effect extrapolates very poorly and ends up being explosive. Here though the larger values the conditional effect fits right into the observed data. (And I swear I did not fiddle with the knot locations, there are just what I picked out offhand to spread them out on the X axis.)
And if you want to do a logistic regression:
smooth.plot_rcs(DC_crime,'TotalLic','BurgClip', knots=[3,7,10,15],
fam=sm.families.Binomial(),marker_alpha=0)I’m not sure how to do this in a way you can get prediction intervals (I know how to do it for Gaussian models, but not for the other glm families, prediction intervals probably don’t make sense for binomial data anyway). But one thing I could expand on in the future is to do quantile regression instead of glm models.
Smooth Plots by Group
Sometimes you want to do the smoothed regression plots with interactions per groups. I have two helper functions to do this. One is group_rcs_plot. Here I use the good old iris data to illustrate, which I will explain why in a second.
#Superimposing rcs on the same plot
iris = sns.load_dataset('iris')
smooth.group_rcs_plot(iris,'sepal_length','sepal_width',
'species',colors=None,num_knots=3)If you pass in the num_knots argument, the knot locations are different for each subgroup of data (which I like as a default). If you pass in the knots argument and the locations, they are the same though for each subgroup.
Note that the way I estimate the models here I estimate three different models on the subsetted data frame, I do not estimate a stacked model with group interactions. So the error bands will be a bit wider than estimating the stacked model.
Sometimes superimposing many different groups is tough to visualize. So then a good option is to make a set of small multiple plots. To help with this, I’ve made a function loc_error, to pipe into seaborn’s small multiple set up:
#Small multiple example
g = sns.FacetGrid(iris, col='species',col_wrap=2)
g.map_dataframe(smooth.loc_error, x='sepal_length', y='sepal_width', num_knots=3)
g.set_axis_labels("Sepal Length", "Sepal Width")And here you can see that the not locations are different for each subset, and this plot by default includes the original observations.
Using the Formula Interface for Plots
Finally, I’ve been experimenting a bit with using the input in a formula interface, more similar to the way ggplot in R allows you to do this. So this is a new function, plot_form, and here is an example Poisson linear model:
smooth.plot_form(data=DC_crime,x='TotalLic',y='TotalCrime',
form='TotalCrime ~ TotalLic',
fam=sm.families.Poisson(), marker_size=12)You can see the explosive effect I talked about, which is common for Poisson/negative binomial models.
Here with the formula interface you can do other things, such as a polynomial regression:
#Can do polynomial terms
smooth.plot_form(data=DC_crime,x='TotalLic',y='TotalCrime',
form='TotalCrime ~ TotalLic + TotalLic**2 + TotalLic**3',
fam=sm.families.Poisson(), marker_size=12)Which here ends up being almost indistinguishable from the linear terms. You can do other smoothers that are available in the patsy library as well, here are bsplines:
#Can do other smoothers
smooth.plot_form(data=DC_crime,x='TotalLic',y='TotalCrime',
form='TotalCrime ~ bs(TotalLic,df=4,degree=3)',
fam=sm.families.Poisson(), marker_size=12)I don’t really have a good reason to prefer restricted cubic splines to bsplines, I am just more familiar with restricted cubic splines (and this plot does not illustrate the knot locations that were by default chosen, although you could pass in knot locations to the bs function).
You can also do other transformations of the x variable. So here if you take the square root of the total number of licenses helps with the explosive effect somewhat:
#Can do transforms of the X variable
smooth.plot_form(data=DC_crime,x='TotalLic',y='TotalCrime',
form='TotalCrime ~ np.sqrt(TotalLic)',
fam=sm.families.Poisson(), marker_size=12)
In the prior blog post about explosive Poisson models I also showed a broken stick type model if you wanted to log the x variable but it has zero values.
#Can do multiple transforms of the X variable
smooth.plot_form(data=DC_crime,x='TotalLic',y='TotalCrime',
form='TotalCrime ~ np.log(TotalLic.clip(1)) + I(TotalLic==0)',
fam=sm.families.Poisson(), marker_size=12)Technically this “works” if you transform the Y variable as well, but the resulting plot is misleading, and the prediction interval is for the transformed variable. E.g. if you pass a formula 'np.log(TotalCrime+1) ~ TotalLic', you would need to exponentiate the the predictions and subtract 1 to get back to the original scale (and then the line won’t be the mean anymore, but the confidence intervals are OK).
I will need to see if I can figure out patsy and sympy to be able to do the inverse transformation to even do that. That type of transform to the y variable directly probably only makes sense for linear models, and then I would also maybe need to do a Duan type smearing estimate to get the mean effect right.